이 포스팅은 [KUOCW] 한정현 교수님 강의 13장 - Character Animation을 듣고 정리한 내용입니다.
선형대수학의 기초적인 지식이 필요합니다.
지난 시간까지는 어떻게 화면에서 지금까지 배운 transform들에 의해 물체가 작용하는지 보이는지, 배웠습니다.
이번 장에서는 object 단위라기보다는 더 복합적인 매쉬(캐릭터)를 그래픽스에서의 애니메이션을 어떻게 다루는 가에 대한 설명입니다.
- Skeleton
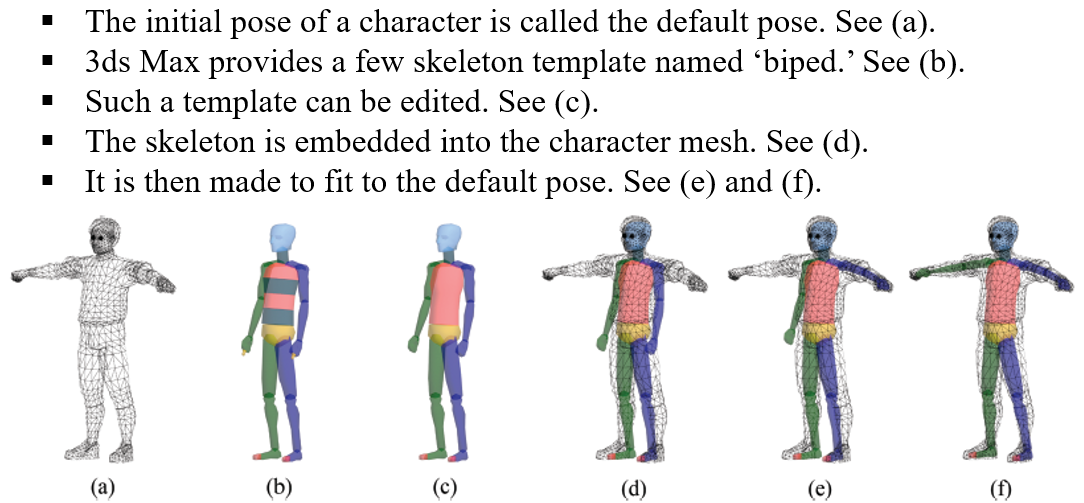
애니메이션에서 캐릭터를 다루는 가장 유명한 방법은 스켈레톤을 사용한 방식입니다. 우리 몸에서 뼈가 움직임의 범위를 결정하듯 아래 사진같이 매쉬로만 이루어진 (a)에 스켈레톤(b)나 좀 더 간략한 스켈레톤인 (c)를 (d)같이 임베딩(위치)시킨 뒤, (e)와 (f) 과정을 통해 매쉬와 매칭 시킵니다. 그리고 이 스켈레톤과 매쉬 간 상호작용은 모두 매트릭스 계산을 통해 이루어지는데요. 앞으로 이에 대해 알아볼 것입니다.
- Skeleton hierarchy
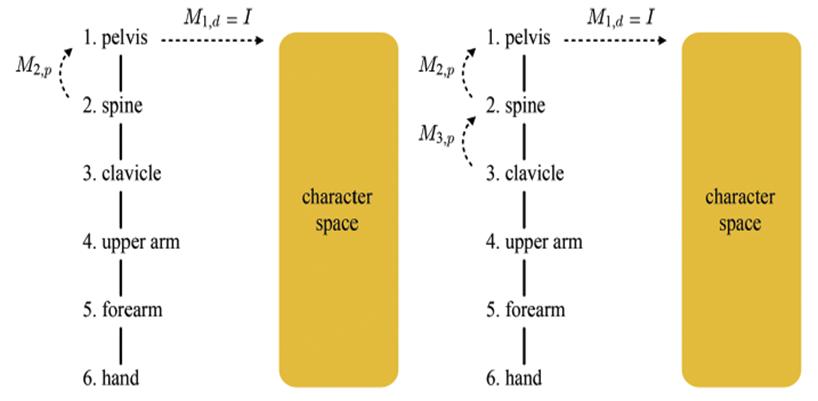
먼저 스켈레톤을 어떻게 디자인 했는지에대해 먼저 알아보겠습니다. 스켈레톤은 ㅅ계층적인 구조를 이루고 있는데요. pelvis라고 불리는 골반이 중심이 되어 양다리, 양팔 그리고 머리로 나누어져 계층을 이루고 있는 것을 아래 사진에서 확인하실 수 있습니다. 강의에서는 왼손에 대한 계층을 예시로 설명 때문에 포스팅 또한 왼손을 기준으로 설명합니다.
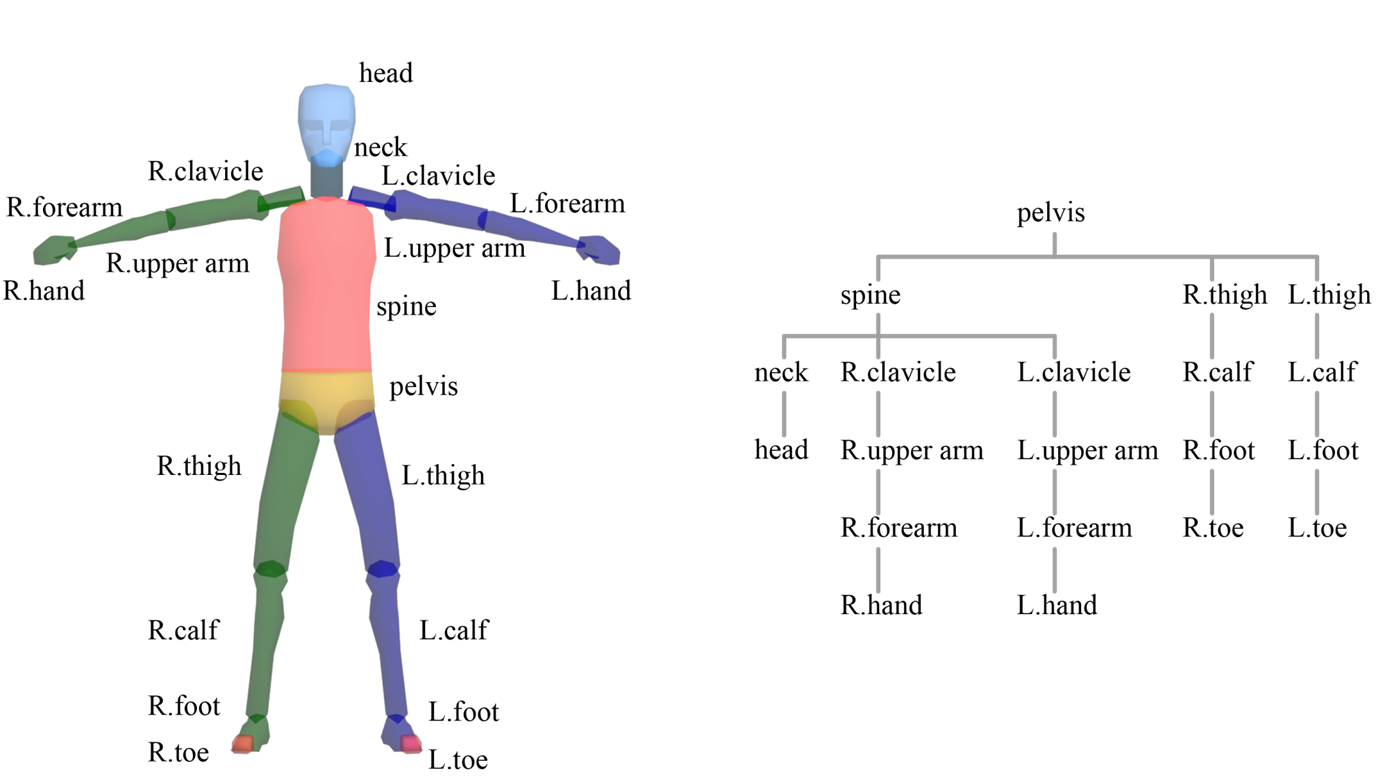
이렇게 계층이 나누어진 이유는 상위 계층(부모 계층)이 움직임을 가져갈 때, 하위 계층(자식 계층)의 스켈레톤에도 영향을 끼치기 때문입니다. 아래 그림처럼 말이죠. 어떤 스켈레톤이 움직임에 영향을 받는 스켈레톤이 하위 계층에 위치하게 디자인 되었다고 이해하시면 될 거 같습니다.
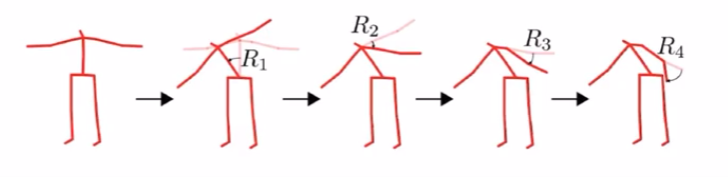
강의와 포스팅에서는 scaling을 제회하고 rotation과 translation을 중심으로 설명합니다. 사람이 움직이는데도 scaling이 갑자기 되진 않으니까요.
- Space Change between Bones
다음으로는 스켈레톤의 움직임에 의한 매쉬를 어떻게 처리해야 되는지에 대해 알아보겠습니다. 스켈레톤을 이용하게 되면 그 바깥의 매쉬는 마치 우리의 피부처럼 스켈레톤에 종속되어 고정됩니다. 하지만 팔꿈치 같은 부분을 생각하면 알 수 있듯 이 매쉬는 피부처럼 스켈레톤을 따라 움직이여야만 하죠.
먼저, 각 스켈레톤과 매쉬와의 관계는 각 관절(joint)에 대한 object space에 대한 정의가 필요합니다. 이때 이 공간을 bone space라고 부릅니다. 왜냐하면 각 joint를 하나의 object라고 생각하시면 될거 같습니다. 하지만 매쉬의 정점들은 bone space에 속해있지 않습니다.
하나의 매쉬가 캐릭터를 이루기 때문에 이 공간(charactor space)에 모두 위치해 있죠. 이때 이 공간의 중심은 pelvis입니다. 하지만 관절이 움직이면 그 관절에 따라 정점들이 움직이도록 계산되어야 할 것입니다. 그러기 위해서는 각 관절에 대한 정점들의 위치를 표현할 수 있어야 하죠. charactor space에서 bone space에 그렇게 표현된 것이 아래 오른쪽 그림입니다.
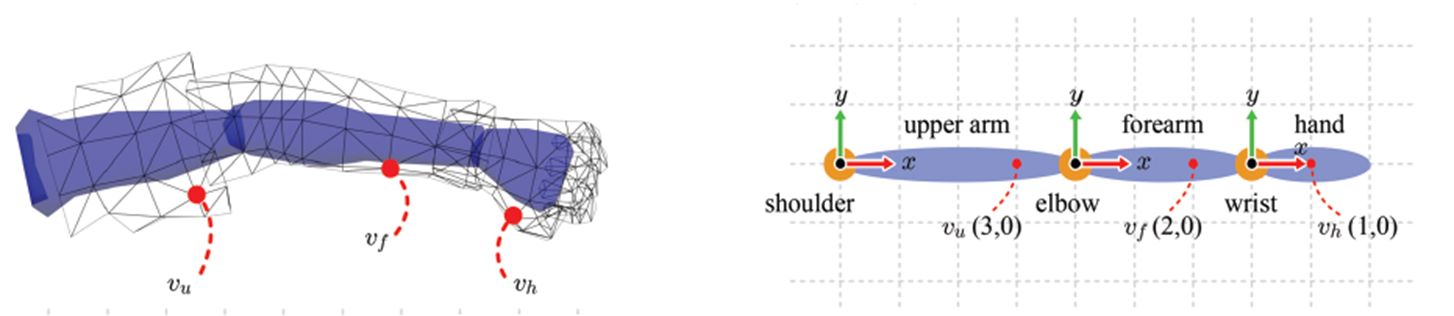
그렇게 하기 위해서 반대로 bone space에서 charactor space로 가는 변환에 대해 생각해 보도록 하겠습니다. 이게 가능하면 그 역변환을 통해 charactor space에서 bone space로 변환이 가능하기 때문이죠. 각 bone space에서 charactor space로 변환한다는 것은 root 스켈레톤인 pelvis로 즉 최종적인 부모 스켈레톤으로 변환한 것과 같습니다. 이는 상위 계층을 계속해서 따라가면 되는 것이죠. 이것을 to-parent transform이라고 부릅니다.
위의 오른쪽 그림을 보면 v_f는 elbow에 대한 bone space기준으로 (2,0)이라는 좌표가 설정된 것을 볼 수 있습니다. 이를 부모 계층의 관절인 shoulder로 옮기기 위해서는 x축으로 4칸의 translation이 필요한 것을 눈금으로 확인할 수 있죠. 이를 아래 수식과 같이 표현할 수 있습니다. 이때 M_f,p의 의미는 elbow 관절의 to-parent transform matrix라는 의미입니다.
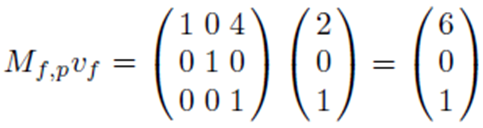
이런 식으로 hand 관절에서 정의된 v_h도 hand->elbow 그리고 elbow->shoulder 변환 matrix를 이용하여 변환이 아래 수식과 같이 가능하죠. 당연히 연립하여 아래 세 번째 줄처럼 표현도 가능합니다.
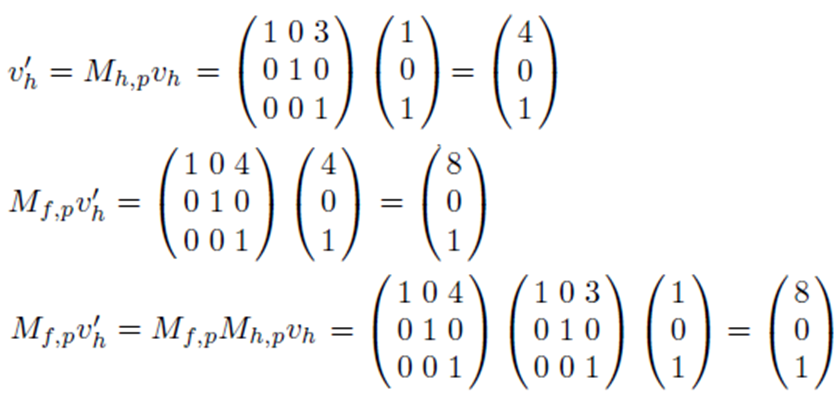
- Character Space to Bone Space

위 처럼 각 계층 구조를 따라 각 bone space 간 변환이 가능함을 보였습니다. 이렇게 root bone space인 pelvis까지 변환을 할 수 있는데, 몇 개의 계층을 통과하든 이를 일반화 표현할 수 있습니다. i관절에서의 to-parent matrix를 M_i, p 그리고 i관절의 bone space to the character space matrix를 M_i, d라고 한다면 아래와 같이 표현됩니다. 이는 부모 계층의 bone space to the character space matrix를 알고 부모 계층까지의 to-parent matrix를 알면 그 행렬 곱의 결과가가 자식 계층의 bone space to the character space matrix가 된다는 것이죠.
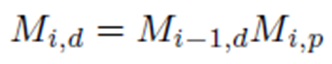
이때 pelvis bone space에서 character space로의 변환 행렬은 단위 행렬로 표현되기 때문에, 처음 요구되는 부모 계층의 변환 행렬이 풀린 것입니다. 따라서 자식 계층의 변환 행렬 또한 모두 구할 수 있습니다.
그럼 이제 어떤 bone space에서든 character space로 변환이 가능함을 알았습니다. 그럼 이제 역변환을 이용해 character space의 정점들을 각 bone space로 변환할 수 있음도 알 수 있죠. 그 변환 행렬은 아래와 같이 표현됩니다.
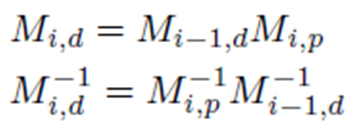
왼쪽 팔에 대한 bone space to the character space matrix도 아래 그림과 같이 표현할 수 있죠.
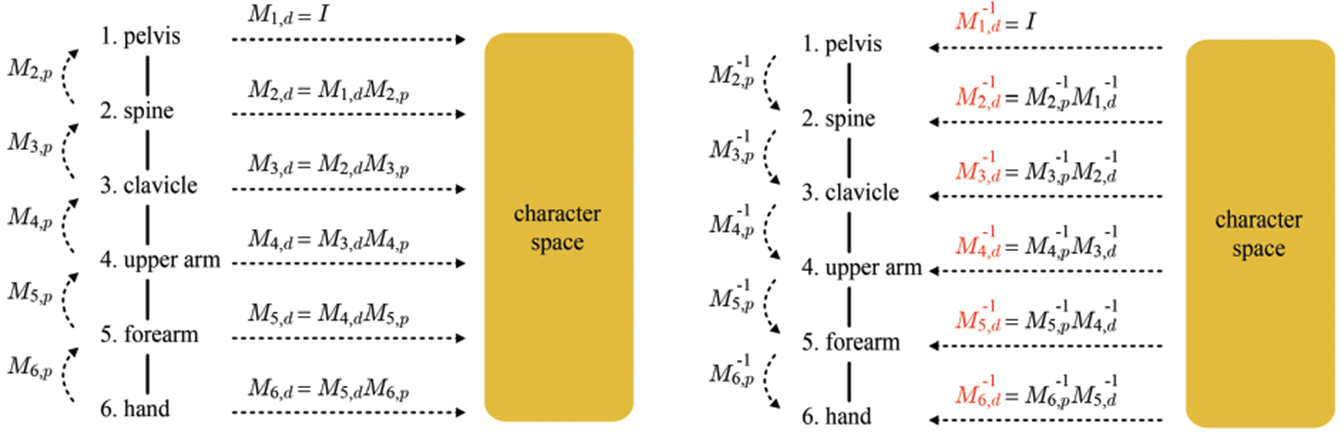
- Forward Kinematics
이제 우리는 관절을 움직이고 관절에 소속되어있는 vertex도 변환시킬 수 있다는 것을 알게 되었습니다. 이 변환 행렬을 통해서 캐릭터를 움직이는 것을 Forward Kinematics라고 합니다. 아래 그림과 같이 elbow를 움직인다면 elbow를 부모 계층으로 하는 자식 계층에 소속된 정점들도 따라 움직이는 것이죠. 먼저 정점 v_5는 bone space에서 회전 변환을 통해 좌표가 v'_5 바뀔 것이고 이를 character space로 변환하면 v''_5가 될 것입니다.
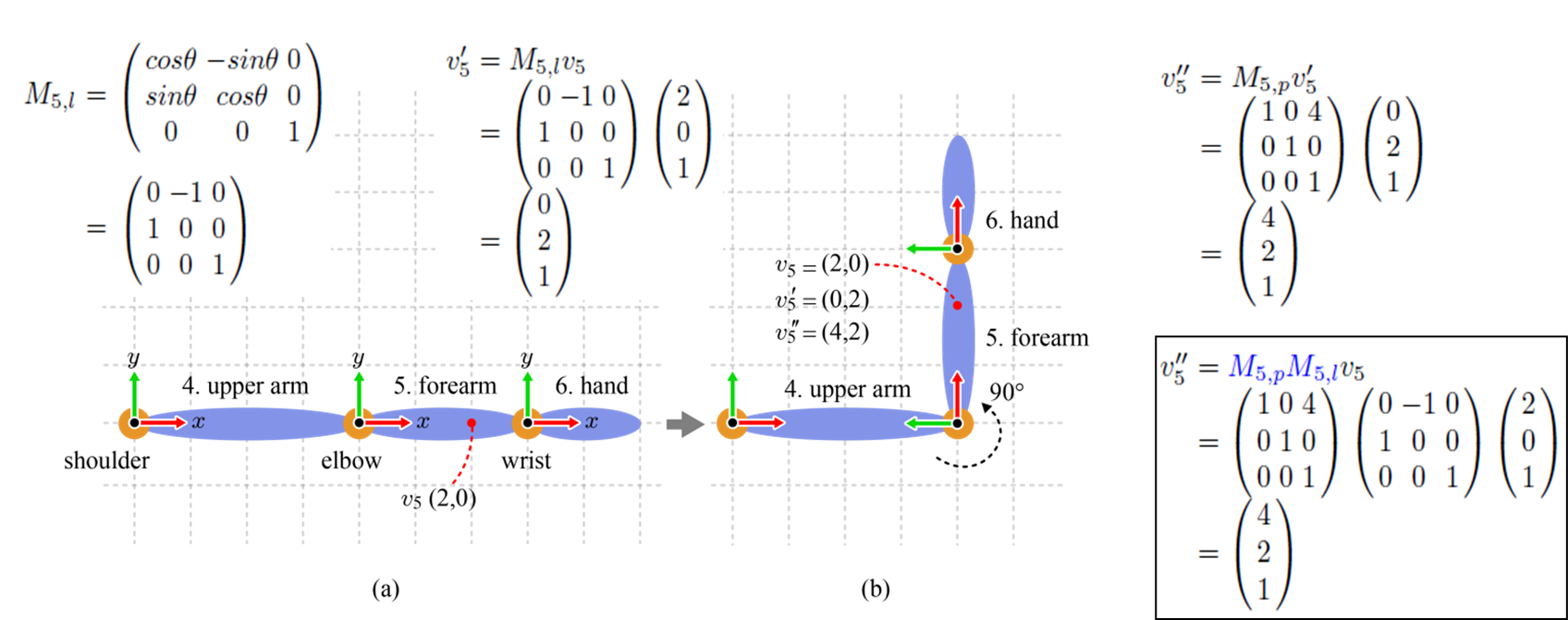
위에서 보시면 아시겠지만, hand에 관절에 속하는 vertex를 움직이는 변환 행렬은 elbow 변환 행렬의 정보에서 유추할 수 있습니다. 이를 일반화하면 아래 수식같이 표현이 가능합니다. M_i-1은 부모 행렬의 animation matrix입니다. M_i, p는 부모 행렬로의 변환 행렬이고, M_i_l은 local transform을 나타냅니다. 즉 현재 계층의 관절에 대한 변환 행렬이죠. 이렇게 하면 현재 bone space에 대한 변환이 어떻게 이뤄져야 되는지 알 수 있습니다.
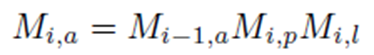
pelvis의 animation은 character라는 object자체를 움직이는 것이기 때문에 pelvis에 대한 Animation Matrix는 아래와 같이 단위행렬로 표현됩니다. 따라서 모든 관절에서 Character space까지의 모든 관절이 표현 가능하죠.

최종적으로, 이렇게 정리하게 되면 한 정점 v가 움직이는 것에 대해서 아래 수식같이 일반화될 수 있습니다. 이렇게 움직이는 정점이 character space에서 어디를 나타내는지 계산할 수 있는 것이죠. 이것이 어떤 관절을 어떻게 움직였을 때 정점 처리가 어떻게 되는 것인지를 계산하는 Forward Kinematics라고 할 수 있습니다.
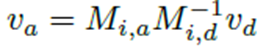

- Skinning
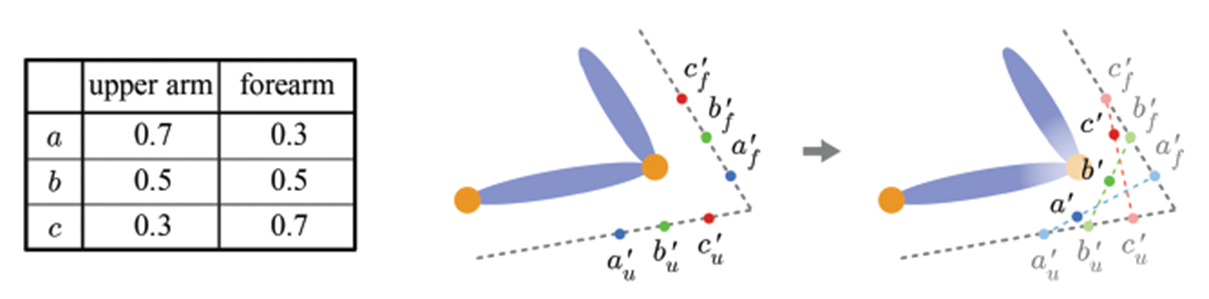
하지만 위와 같은 Forward Kinematics를 사용하게 되면 문제점이 있습니다. 바로 vertex가 부자연스럽게 표현된다는 것이죠. 아래 그림과 같이 upper arm에 정점 a가 속하고 forearm에 b와 c가 속한다고 가정하고 elbow를 움직이게 되면, 오른쪽 그림같이 정점은 우리의 생각과 다른 곳에 위치하는 것을 알 수 있습니다.

이 문제점을 해결하기 위해서 그래픽스에서는 하나의 정점이 하나의 bone space에 속한 것이 아니라 여러 관절에 속하게 하여 이 문제를 해결합니다. 아래 왼쪽 표와 같이 각 정점들이 그 비율에 따라 bone space에 속하게 되고 변환 시 그 비율을 참고하여 가중치를 더해주어 그 위치를 결정합니다. 보관법과 같은 방식으로 그 위치를 결정하는 것이죠.
이 방법을 그래픽스에서 skinning이라고 부르는 것 같습니다. 보통 하나의 정점은 4개의 bone space에 속하게 계산하고, 모바일 같은 적은 계산양을 요구하는 곳에서는 보다 적은 bone space를 고려합니다. 이 파이프 라인은 아래와 같이 표현되었는데요. skinning 알고리즘은 vertex shader에서 이루어집니다. 한 정점이 어디에 속하는지를 나타내는 palette indices와 각 bone space에 얼마나 속해 있는지를 나타내는 blend weights는 rigging 단계에서 생성되어 vertex array에 attribute로 저장됩니다. 또한 matrix palette는 정점에 따라 변하지 않기 때문에 uniform으로 제공됩니다.
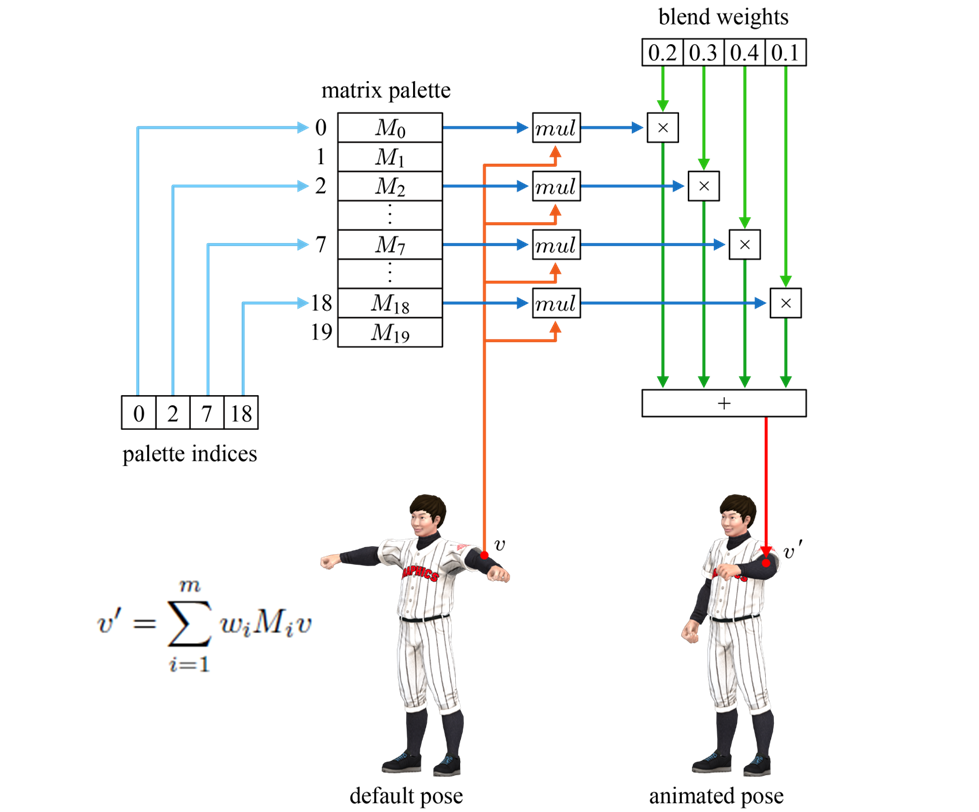
- Inverse Kinematics(IK)
Inverse Kinematics는 앞서 살펴본 Forward Kineatics에 다른 방식의 animation입니다. Forward Kineatics가 관절의 움직임을 먼저 생각하고 정점을 계산하는 Top-Down 방식이었다면, Inverse Kinematics는 어떤 위치로 캐릭터의 end effector(ex. 손, 발)를 위치시키기 위해 관절을 얼마나 움직여야 하는지를 계산하는 Bottom-Up 방식입니다.
여기서는 Degree Of Freedom(DOF)라는 개념이 등장하는데 자유도 뜻으로 한 관절의 움직이는 상태를 나타내기 위한 최소한의 변수를 뜻합니다. 아래 그림을 보면 이해가 쉬운데요. 왼쪽 a는 DOF 가 1이고 오른쪽 b는 DOF가 3입니다.

강의에서는 두 가지 IK 방식을 설명해 주는데요. 처음은 Analytic Solution입니다. 먼저 아래 그림과 같이 T라는 end effector를 G라는 지점에 위치시키고 싶다고 합니다. 그러면 관절을 얼마나 움직여야 되는지에 대한 계산이 요구되죠. 이때 (b)에 나온 대로 삼각함수를 활용하여 elbow가 얼마만큼의 각도가 되어야 G와 동일 선상에 위치되는지를 구합니다. 다음으로 G와 T를 향한 단위 벡터 v_1, v_2를 이용하여 내적과 외적을 통해 얼마만큼 회전해야 하는지, 어떤 축을 기준으로 회전에야 하는지를 알아냅니다. 이렇게 수식적으로 풀어나가는 것을 Analytic Solution이라고 하죠.
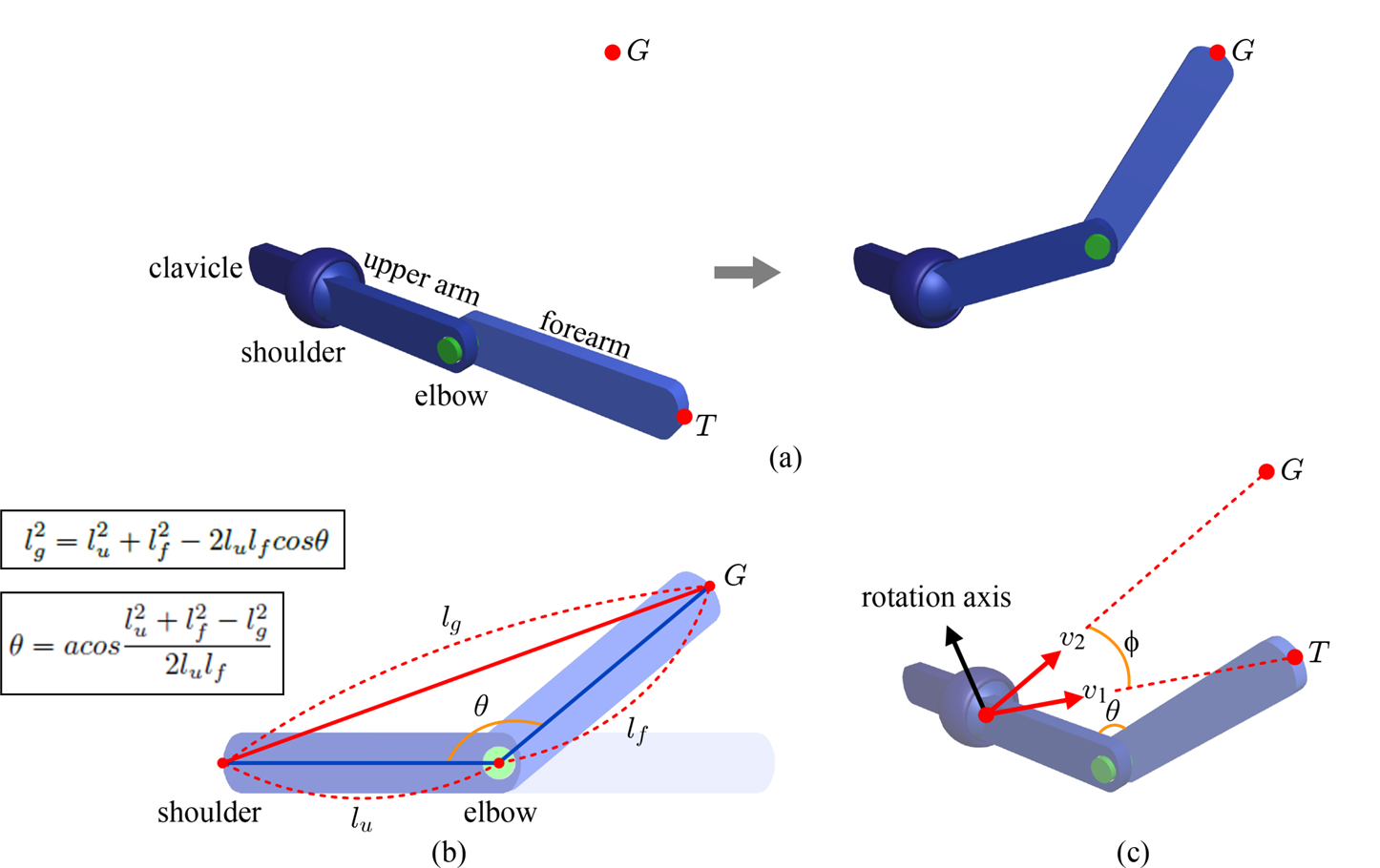
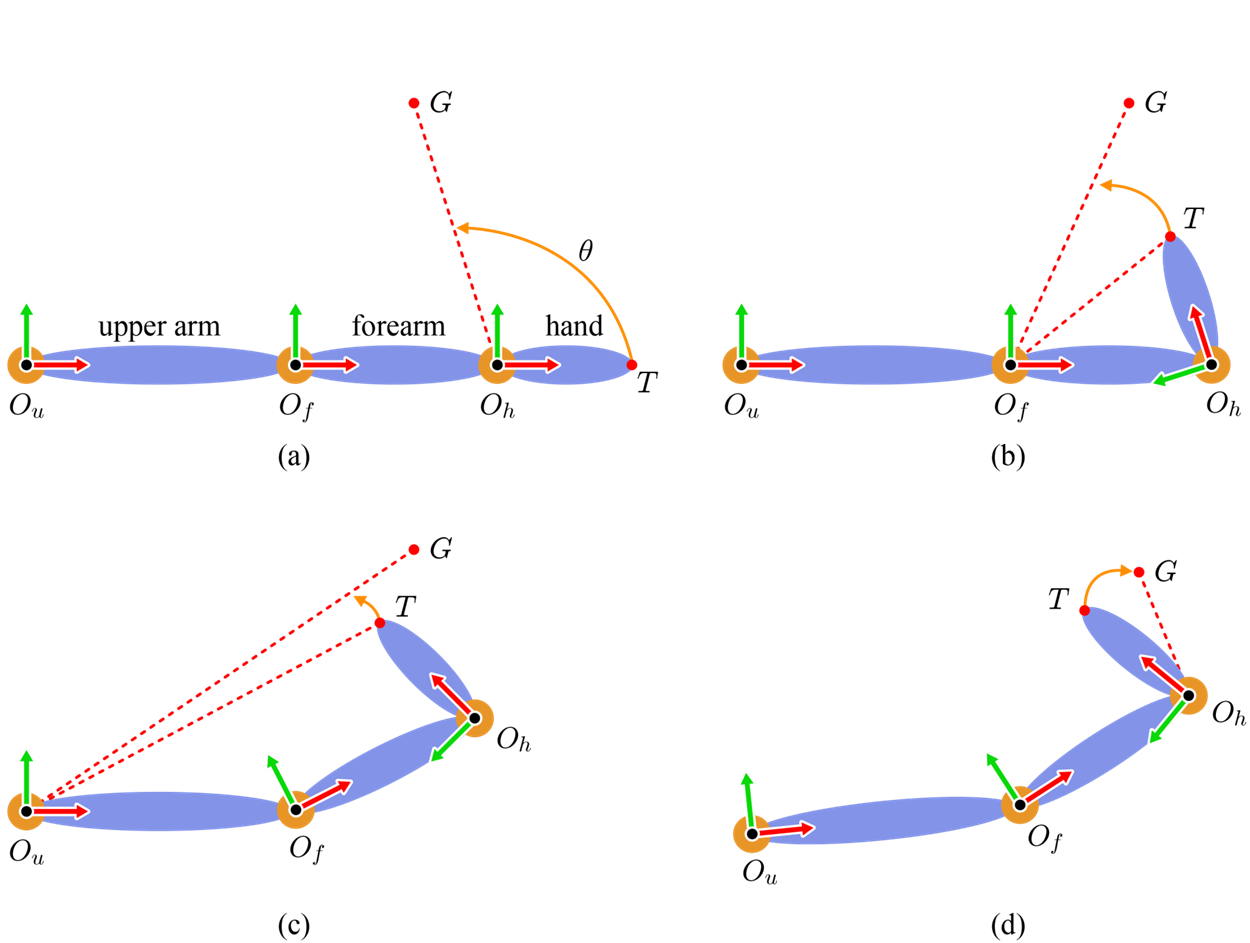
하지만 이런 식으로 방정식을 세우는 것은 쉽지 않다고 합니다. 그렇기 때문에 Cyclic Coordinate Descent라는 다른 방식을 강의에서 설명해줍니다. 이는 위 와같이 수식적으로 관절을 움직이는 것이 아니라 End effector와 가장 가까운 관절부터 차례대로(Cyclic) 목표 지점인 G를 향하게 움직이면서 오차를 수정하는 방식입니다. 이런 방식을 활용하면 딱 한 번씩만 관절을 움직여서 위치시킬 순 없지만 복잡한 계산 없이 빠르게 실행할 수 있습니다. 이때 오차 범위나 반복 횟수에 따라 그 정확도는 변화하게 되죠.
이런 IK방식을 활용하게 되면 특정 목표지점을 따라가는 tracking을 하는데도 활용될 수 있죠. 아래 사진은 IK방식은 위 와같이 꼭 end effector가 목표 지점에 닿는 위치에 있지 않더라도 적용 가능함을 보여줍니다. 캐릭터의 눈과 왼쪽 손은 빨간 공에 따라 움직이고 있죠.

이렇게 사람 캐릭터를 기준으로 그래픽스에서 animation을 자연스럽게 표현할 수 있음을 알아보았습니다. 막 수학적으로 어렵진 않지만 그 수학적인 디테일이 들어있음을 배우면서 매번 느끼게 되는 거 같습니다.
감사합니다.
References
강의: [KUOCW] 한정현 교수님 강의
https://www.youtube.com/channel/UCfyXTCv0QlZxG1S1rteGI7A
강의 자료: 한정현 교수님 연구실 홈페이지
http://media.korea.ac.kr/books/
'컴퓨터 그래픽스' 카테고리의 다른 글
| 컴퓨터 그래픽스 - Shadow Mapping([KUOCW] 한정현 교수님 강의) (0) | 2022.02.07 |
|---|---|
| 컴퓨터 그래픽스 - Normal Mapping([KUOCW] 한정현 교수님 강의) (0) | 2022.02.06 |
| 컴퓨터 그래픽스 - Screen-space Object Manipulation part 2. Bounding Volume and ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.21 |
| 컴퓨터 그래픽스 - Screen-space Object Manipulation part 1. Object Picking ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.21 |
| 컴퓨터 그래픽스 - Quaternion ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.20 |



