이 포스팅은 [KUOCW] 한정현 교수님 강의 14장 - Normal Mapping을 듣고 정리한 내용입니다.
선형대수학의 기초적인 지식이 필요합니다.
이전에 Vertex Normal에 대해서 배워보았습니다. 그리고 Lighting에 대해서도 배웠죠.
이 두 가지를 이용해서 보다 간결하게 Texture를 자연스럽게 표현하는 것을 이번 강에서 설명합니다.
관련된 포스팅은 아래와 같습니다.
2022.01.17 - [컴퓨터 그래픽스] - 컴퓨터 그래픽스 기초 - Vertex representation, Affine transform([KUOCW] 한정현 교수님 강의)
2022.01.19 - [컴퓨터 그래픽스] - 컴퓨터 그래픽스 기초 - Fragment Shader part 1. Texturing ([KUOCW] 한정현 교수님 강의)
2022.01.19 - [컴퓨터 그래픽스] - 컴퓨터 그래픽스 기초 - Fragment Shader part 2. Phong Lighting ([KUOCW] 한정현 교수님 강의)
- Bumpy Surface(돌출 표면)
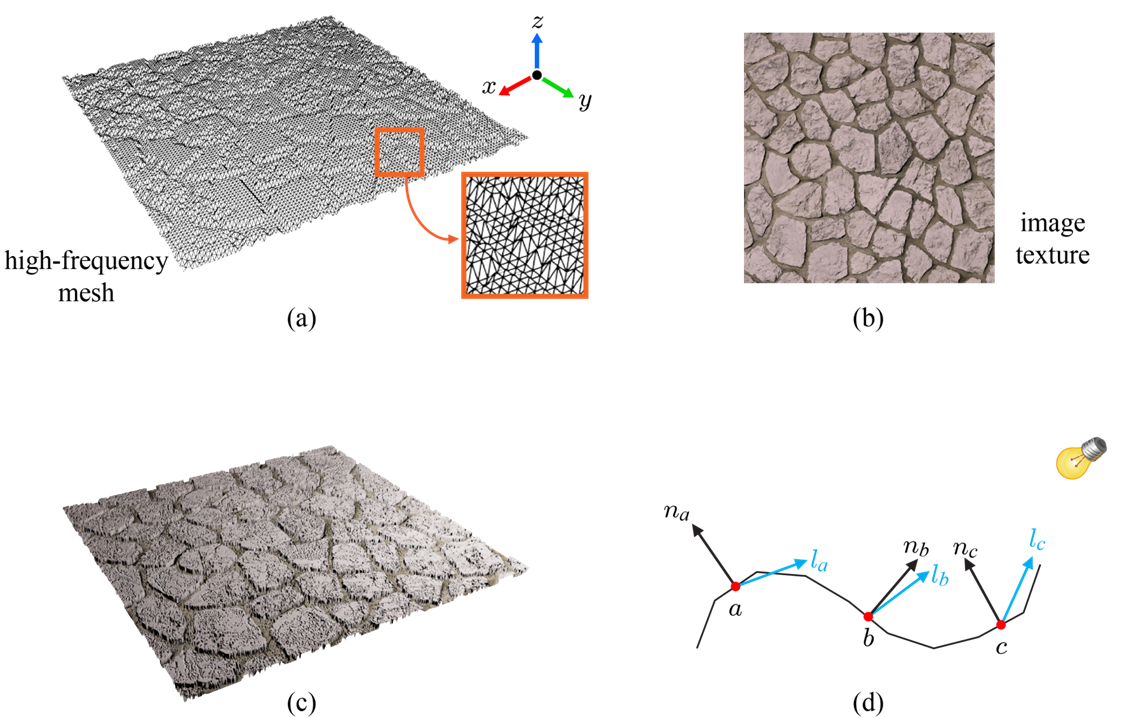
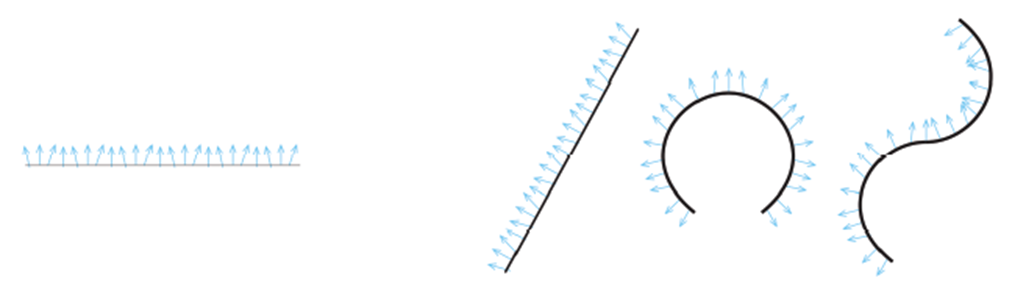
normal mapping이 등장하게 된 배경은 vertex로 미세한 표면을 다 표현하기에는 요구되는 메모리 혹은 처리량이 부담되기 때문입니다. 예시로 아래와 같이 오돌토돌한 표면을 가진 Bumpy Surface을 들겠습니다. 이러한 (a)같이 high-frequency polygon mesh는 여러 vertex들이 미세하게 표현되어있습니다. 여기에 (b) texture를 적용하면, 이러한 vertex의 normal의 방향이 (d)처럼 다양하기 때문에 빛을 비추면 그 표면이 (c)처럼 표현되는 것이죠.
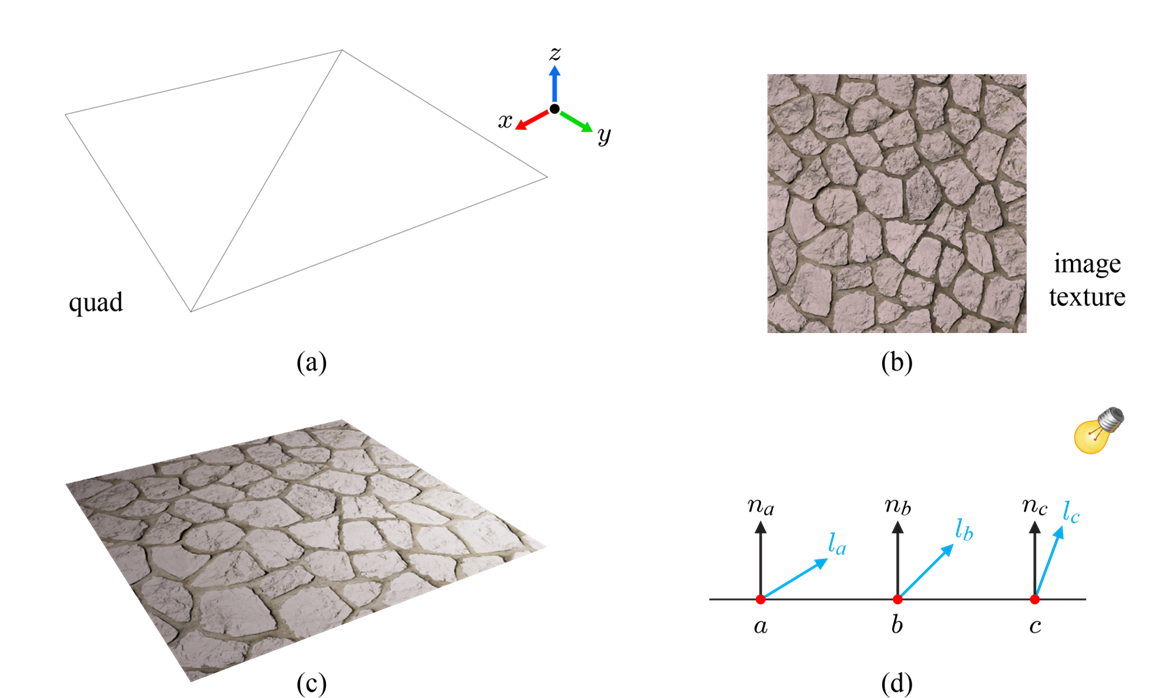
하지만 계산량을 줄이려고 극단적으로 vertex를 줄이면 아래 (a)같이 mesh를 만든다고 가정하면 그 표면이 위에서 처럼 세세하게 표현되지 않을 것입니다. Normal Vector가 비교적 단순하게 구성되어있기 때문이죠.
- Normal Mapping
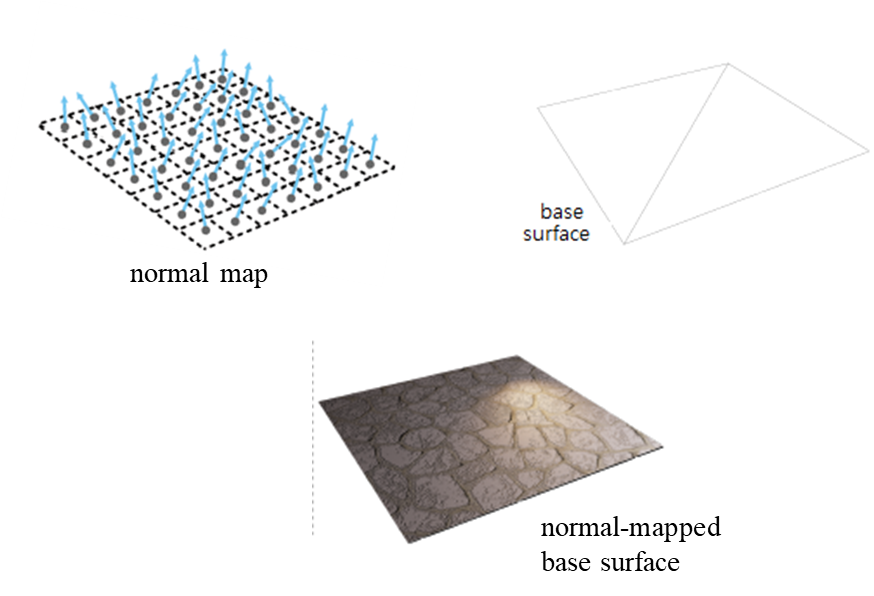
그래픽스에서는 빛과 normal vector에 의해 그 표면이 표현되는 점을 착안해서 vertex는 비교적 단순하지만 normal vector를 vertex에 의해서가 아니라 따로 복잡하게 표현해서 high-frequency 패턴을 표현하는 트릭을 사용합니다. 바로 아래 그림처럼 복잡한 mesh에서 표현되는 normal vector와 유사하게 평평하고 단순한 mesh에서의 normal vector도 mapping을 시켜주는 것이죠.

그러기 위해서 해당 fragment에 표현할 색상을 정해주는 texture map과 같이 normal map이라는 개념이 등장합니다. 아아래 그림은 normal map과 단순한 mesh인 base surface를 결합하여 미세한 표면을 표현한 normal-mapped base surface를 나타냅니다.
- How to make normal map
Normal map을 만들기 위해서는 우선 Height map 또는 Height field라는 개념을 알 필요가 있습니다. High-frequency surface의 높이 정보를 h(x, y), 즉 x, y 좌표에 해당하는 z값을 활용한 것이 height map입니다. 이 height map은 [0,255]의 범위의 값을 갖고 있는 하나의 채널이기 때문에 gray scale로도 표현됩니다.
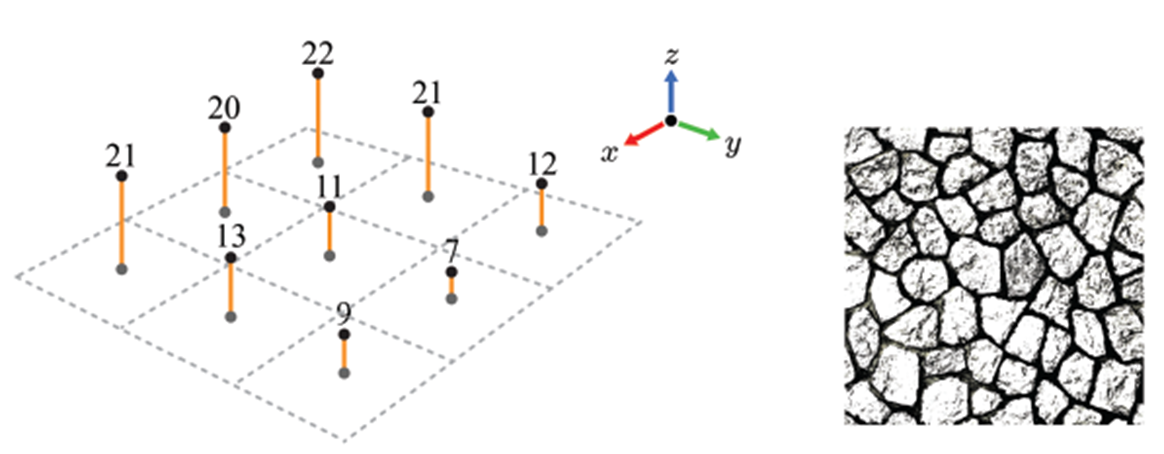
혹은 이 height map을 texture만 가지고 만들기도 합니다. 보통은 texture map을 gray scale로 바꾸면 검은색으로 비춰진 부분이 비교적 낮아서 그늘진 부분이라고 여기고 gray scale에서 이는 낮은 값을 나타내기 때문에 이를 height로 여기고 처리하는 것이죠. 하지만 이는 정확한 표현은 아니므로 보정이 필요할 때도 있다고 강의에서는 말합니다.

위의 두가지 방법으로 구해진 Height map을 가지고 이제 각 vertex의 Normal을 표현합니다. normal을 구하는 방법은 이웃한 좌표의 x선상 y선상으로의 벡터를 가운데 그림처럼 빨간색, 초록색 화살표처럼 구합니다. 이 두 벡터의 외적을 통해 두 벡터의 수직 한 방향으로 vector를 구하고 normalize를 통해 길이가 1인 벡터로 나타냅니다.
해당 좌표를 표현하는 곡면의 방정식에서 해당 좌표에 수직한 normal vector를 구하는 것이 가장 정확하겠지만, 계산하기가 어렵기 때문에 이러한 수식을 통해 적당히 근사하여 해당 좌표에서의 normal vector의 방향을 표현하는 것입니다.
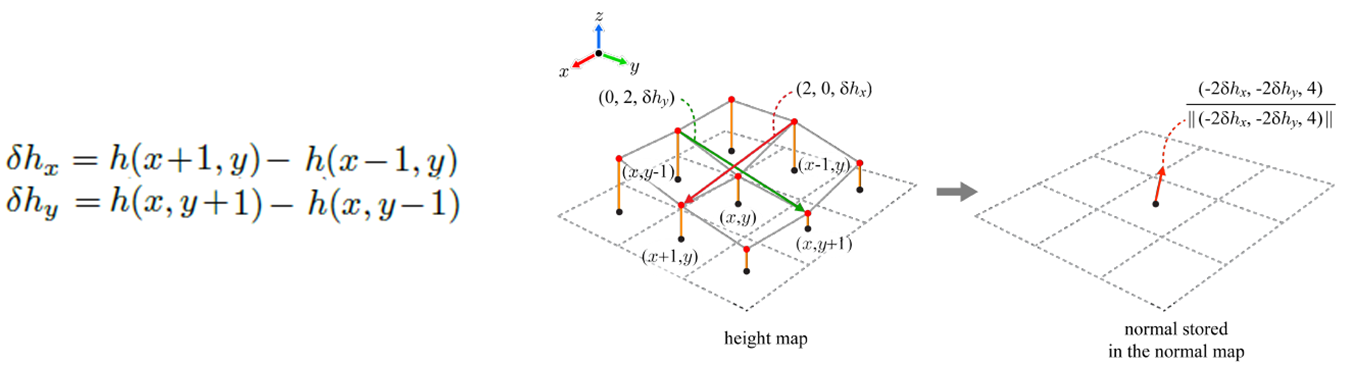
이렇게 만들어진 normal map을 시각화하면 아래 그림의 가운데 수식처럼 [-1,1] 범위로 normalize 해서 표현됩니다. 이때 x, y, z 값은 각 R, G, B 값으로 표현되는데 z값에 해당하는 B(Blue) 값이 보통 다른 값보다 큰 값을 가지기 때문에 normal map은 파란색으로 표현되는 것이 대다수이죠.
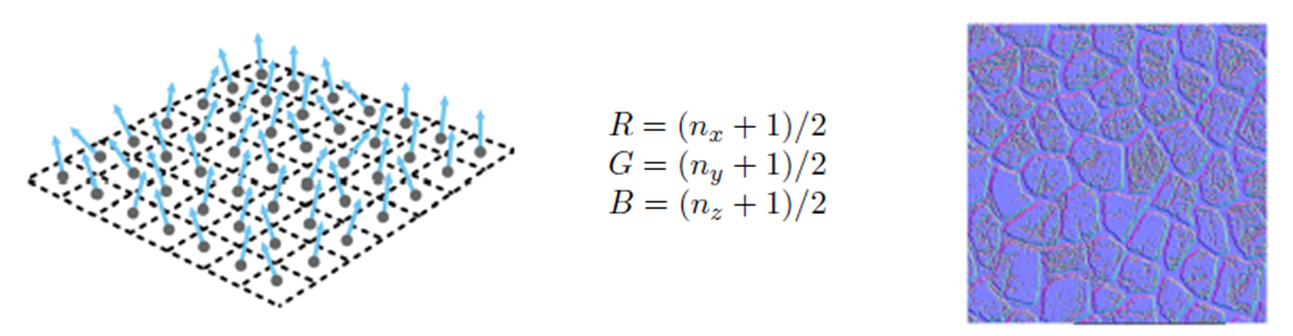
이렇게 구해진 Normal map은 vertex shader가 아니라 texture map처럼 fragment shader에서 처리됩니다. 지금 사용하고자 하는 mesh의 크기와 normal map의 크기가 다르기 때문에 texture map처럼 filtering이 필요하죠. 이러한 개념은 texture과 유사하게 이루어진다고 알고 여기서는 넘어가겠습니다.
이렇게 만들어진 normal map은 이제 fragment shader를 통해 적용되어 lighting을 계산할때 그 값이 적용되어 단순한 mesh에서도 그 normal이 다르게 mapping 되었기 때문에 아래 맨 마지막 줄 그림처럼 미세한 부분까지도 표현된 texturing 효과를 비교적 적은 연산을 통해 나타낼 수 있게 되는 것이죠.
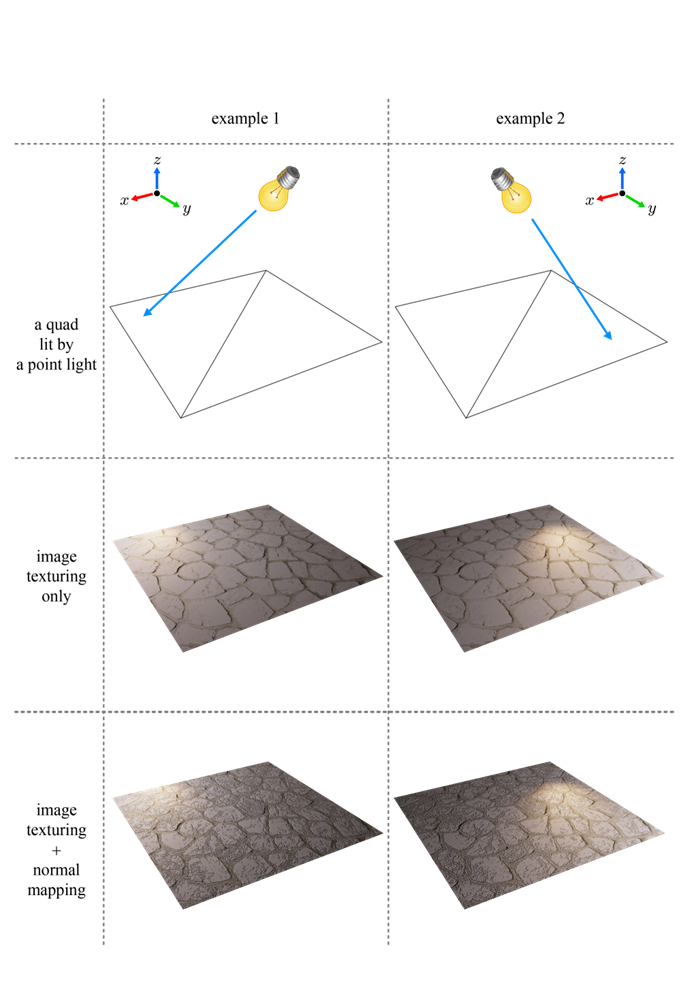
강의에서는 코드까지 설명을 해주기 때문에 코드가 궁금하시면 맨 아래 링크에서 참고 부탁드립니다.
- Tangent-space Normal Mapping
Tangent-space Normal Mapping은 texturing도 다양한 곡면에 적용이 가능한 것 처럼 normal map 또한 적용이 가능하다는 것을 보여줍니다.
그러기 위하서는 추가적인 계산이 요구되는데, 여기서 나오는 개념이 tangent space입니다. 이는 접선(tangent line) 또는 접면(tangent plane)을 말합니다. 아래 그림처럼 구의 한점 p 또는 q에서는 그 접면을 나타낼 수 있는데 각 접면마다 하나의 Tangent vector T(tangent)와 또 다른 Tangent vector B(bitangent)를 나타냅니다. 이를 이용해 해당 접면에 수직인 normal vector N을 구할 수 있죠.

이를 T,B,N을 이용하여 한 점에 적용되는 normal map의 normal을 그 모양이 다르더라도 적용합니다. 바로 T, B, N을 좌표계 삼아 얼마큼 좌표계와 벗어나 있는지 상대적으로 계산하여 나타내는 것이죠. 다시 말하자면 normal map에도 tanget space가 있을 것입니다. 그리고 구체에도 각 지점마다 tangent space가 있죠. 이를 이용해 normal map의 tanget space에서 해당 normal이 좌표축과의 상대적 위치를 구체의 tangent space에서도 표현한다는 것이죠.
하지만 이렇게 나타내면, 문제점이 발생합니다. 빛의 효과를 계산하기 위해서는 광원을 향하는 light vector와 normal vector의 내적 계산이 요구되는데, light vector는 각 점마다 정의된 좌표축을 가진 tangent space에, light vector는 world space에 정의되어 있다는 것이죠.
이떄 T, B, N 정보는 vertex shader의 기존 normal vector를 이용하여 계산이 가능합니다. 그리고 서로 다른 좌표 계간 rotation 변환은 비교적 간단함을 우리는 배웠습니다. 이를 이용하여 Tagent spaced의 basis로 world space에서 tangent space로의 변환을 나타내어 light source를 tangent space에서 정의하여 계산이 가능하게 하여 처리할 수 있습니다. 이렇게 되면 이제 빛에 대한 연산은 모두 tangent space에서 이루어지는 것이죠. 어떻게 rendering 단계까지 명확하게 변환되어 적용되는지는 정확하게 안나와있어 내부적으로 처리된다고 이해했습니다.
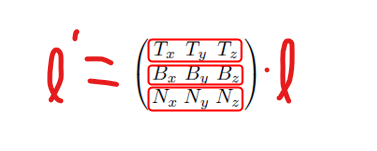
이렇게 tangent space의 개념을 적용해 계산하게 되면 평면이 아닌 다른 형태에 대해서도 빛의 효과를 계산할 수 있게 되었습니다. 이렇게 되면 Normal map은 Texture map처럼 사각형의 형태지만 아래 그림처럼 다양한 형태의 mesh에도 적용이 가능하죠. 이 부분도 강의에서는 코드까지 설명해 주시기 때문에 강의 내용 참고하시면 좋을거 같습니다.
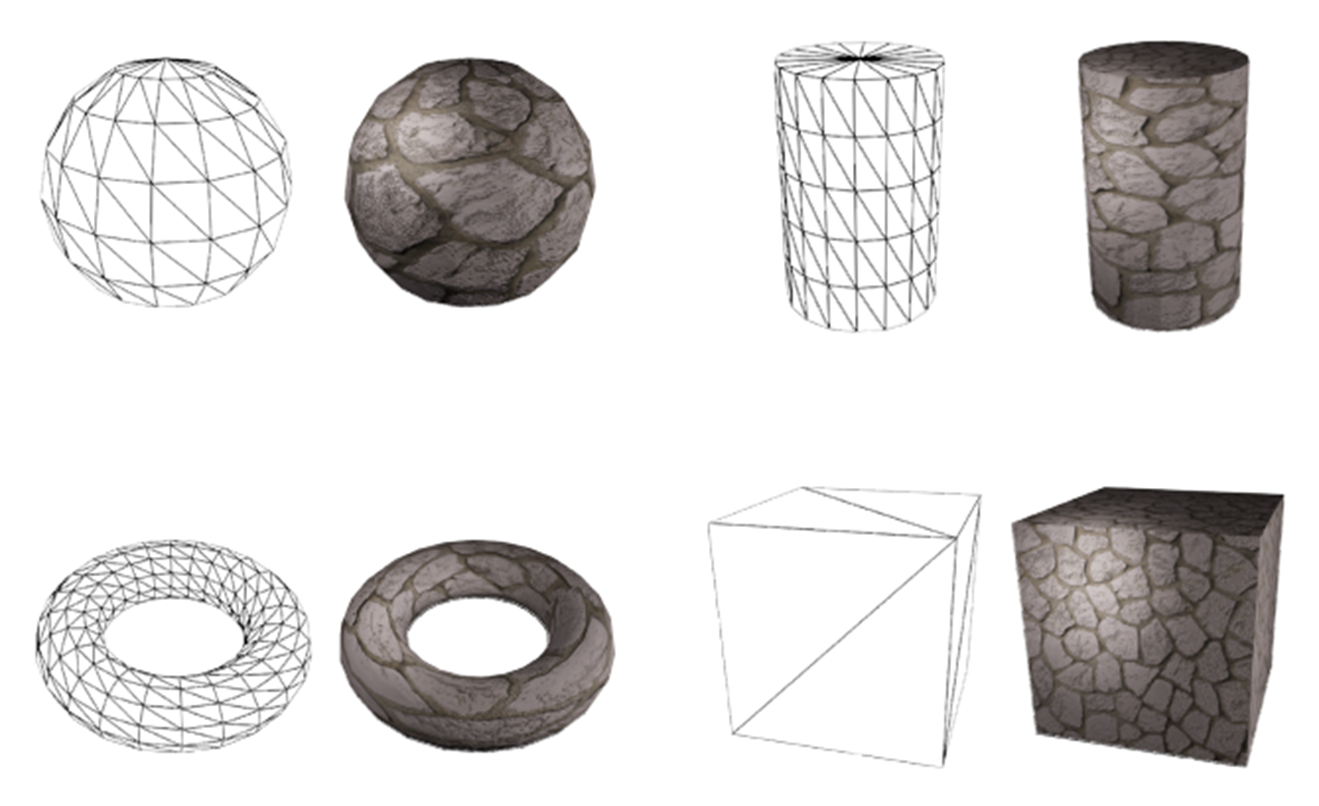
이렇게 이번 포스팅에서는 normal mapping을 이용해 정점들을 이용해 복합적인 형태를 표현하지 않아도, normal vector를 이용해서 적은 연산으로 입체적인 효과를 줄 수 있음을 배웠습니다.
감사합니다.
References
강의: [KUOCW] 한정현 교수님 강의
https://www.youtube.com/channel/UCfyXTCv0QlZxG1S1rteGI7A
강의 자료: 한정현 교수님 연구실 홈페이지
http://media.korea.ac.kr/books/



