이 포스팅은 [KUOCW] 한정현 교수님 강의 11장 - Quaternion을 듣고 정리한 내용입니다.
선형대수학과 복소수의 기초적인 지식이 필요합니다.
지난 포스팅까지는 그래픽스에서 어떻게 화면의 픽셀을 만들어 우리에게 보여주는지 그 Rendering pipeline을 배웠습니다. 이제부터는 지금까지 배운 그래픽스 공간에서 다양한 기능들이 어떻게 작동하는지 알아보겠습니다.
- Keyframe Animation
어떤 애니메이션을 만들려면 매 프레임을 연속적으로 보이게 제작해야 할 것입니다. 그래픽스에서도 매 프레임을 만들어 주어야 할까요? 아닙니다. Keyframe이라고 부르는 주요한 부분(꺾이거나 변화하는 구간)을 표시해주고, 그 사이의 in-between frame을 보간(interpolate)하는 방법을 통해 그래픽스는 보다 쉽게 애니메이션을 자동적으로 만들 수 있죠. 아래 그림은 2D 공간에서 keyframe의 좌표와 방향벡터 p_0, θ_0, p_1, θ_1으로 보간을 통해 in-between frame을 나타내는 수식과 그림을 보여줍니다.

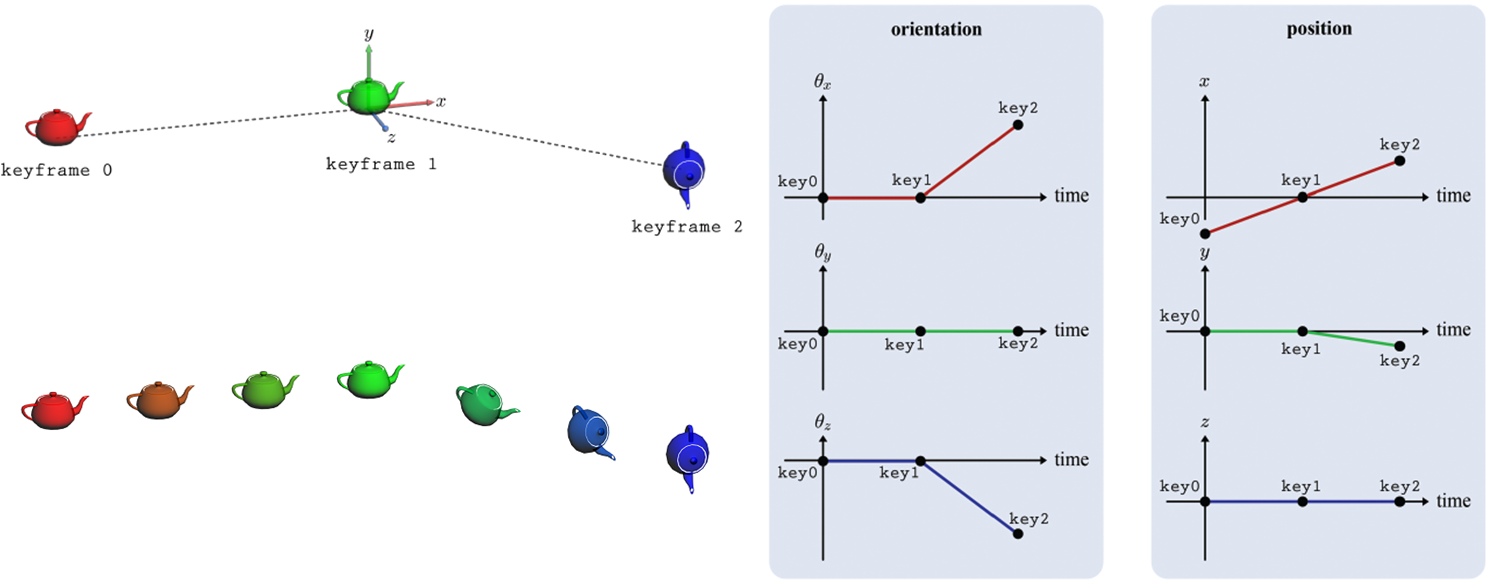
아래 3D 그래픽스 공간을 표현한 그림을 예시로 보겠습니다. 아래 그림은 3가지 keyframe이 있고 보간을 통해 그 아래 in-between frame을 만든 모습입니다. 좌표계를 통해 보여주면 그 오른편에 나와있는 그림과 같죠. keyframe 사이의 frame 값을 시간을 기준으로 weighted sum을 통해 알아내는 것입니다. 그림은 위치, 각도 그리고 색상까지 보간이 될 수 있음을 보여줍니다.
- A Problem of Euler Angles
2022.01.17 - [컴퓨터 그래픽스] - 컴퓨터 그래픽스 기초 - Vertex representation, Affine transform([KUOCW] 한정현 교수님 강의).
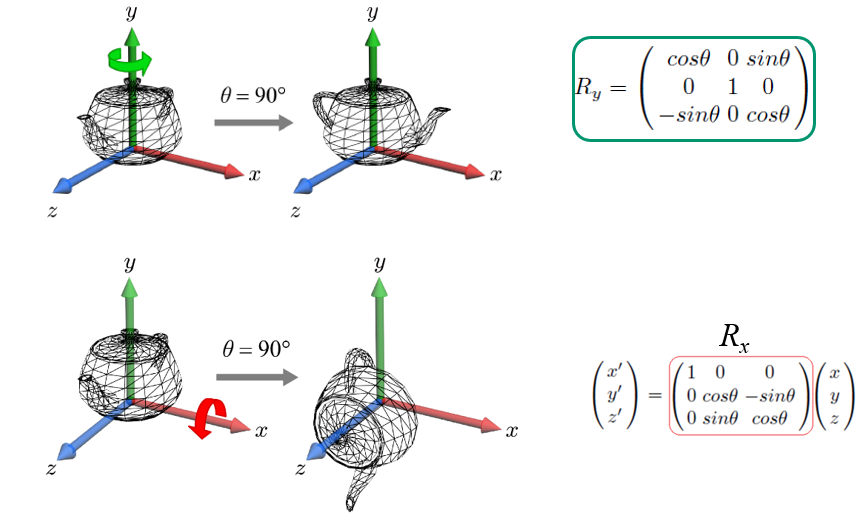
앞서 우리는 affine transform에 대해서 배웠습니다. 그중 rotation도 존재했죠. 이때의 rotation은 world transformation 4x4 matrix [L | t]에서 3x3 matrix L에 아래와 같이 표현할 수 있었죠. 이때 각 축을 기준으로 해서 회전을 하였죠. 또한 각 축에 대한 회전 행렬 R_x, R_y는 R_xy = R_x*R_y로 하나의 행렬로도 표현이 가능했죠(순서는 바뀌면 안 됩니다). 이렇게 각 축을 기준으로 회전하는 각도 θ_x, θ_y, θ_z를 Euler Angle이라고 합니다.
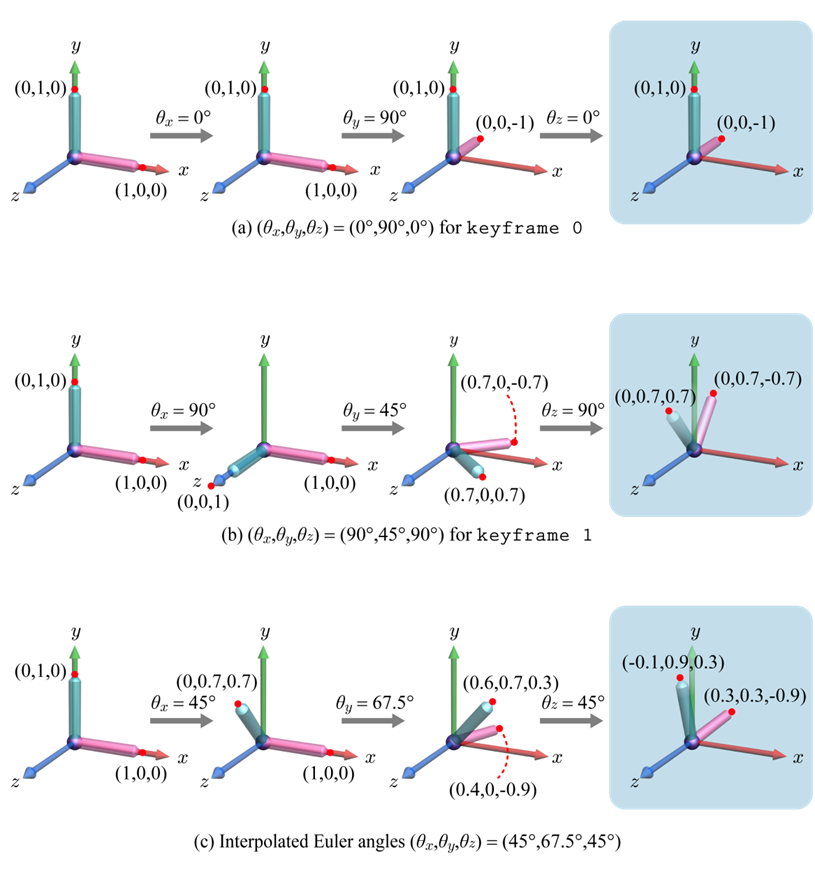
하지만 이렇게 Euler Angle을 기준으로 회전하는 것에는 문제가 있습니다. 저는 가장 짐벌 락 현상이 나올 줄 알았지만, 강의에서는 위의 보간을 예시를 들어 설명합니다. 아래 그림과 같이 첫 번째와 두 번째 줄의 회전 변환 결과 사이를 보간한다고 가정했을 때, 첫 번째와 두 번째 줄의 회전 변환의 결과는 모두 yz-plane 평면상에 있으므로 보간한 결과들 역시 yz-plane 평면상에 있어야 할거 같습니다. 하지만 세 번째 줄의 결과를 보면 그렇지 않습니다. 이렇듯 Euler Angle를 사용하면 문제가 생길 수 있는 것이죠.
- Quaternion의 정의와 성질
하지만 Quaternion은 위의 문제를 해결할 수 있습니다. Quaternion이란 4차원 벡터를 뜻하는 말입니다. 한국말로는 4원수라고도 하죠. 여기서 복소수의 개념이 등장합니다. 아래와 같이 Quaternion을 정의하죠 왼쪽부터 3가지 항은 각각 다른 허수 축을 가지는 허수부로 오른쪽은 실수부를 나타냅니다. 세 가지 허수부를 줄여서 _v로 나타내기도 하죠.
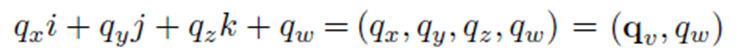
그리고 기본적인 두 Quaternion의 연산과 각 축에 대한 성질 은은 아래와 같습니다.
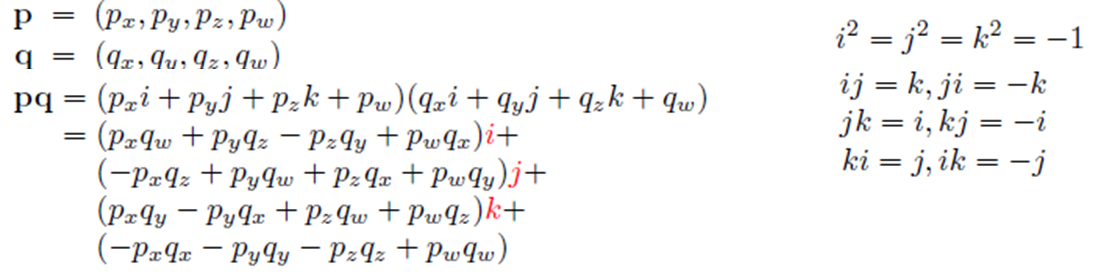
또한 Quaternion의 켤례 복소수와 크기는 아래와 같이 표현되죠.
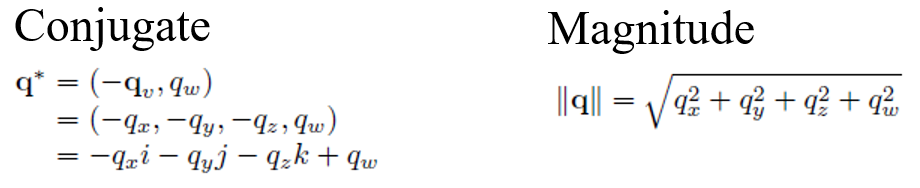
- Quaternion을 이용한 회전
우선 복소수를 이용해 2D회전에 먼저 적용시켜 보겠습니다. 아래 그림과 같이 점 p(x, y)에서 점 p'(x', y')로 θ만큼 회전을 한다고 합시다. 이때 p를 복소수를 이용하여 x+yi로 나타내고 또 θ를 이용해 cosθ+sinθi로 하고 pq를 연산하면 실수부는 x'을 나타내고 허수부는 y'을 타나 내는 것을 확인할 수 있죠. 신기하게도 복소수를 이용해 회전에 관련된 값을 계산할 수 있는 것입니다.
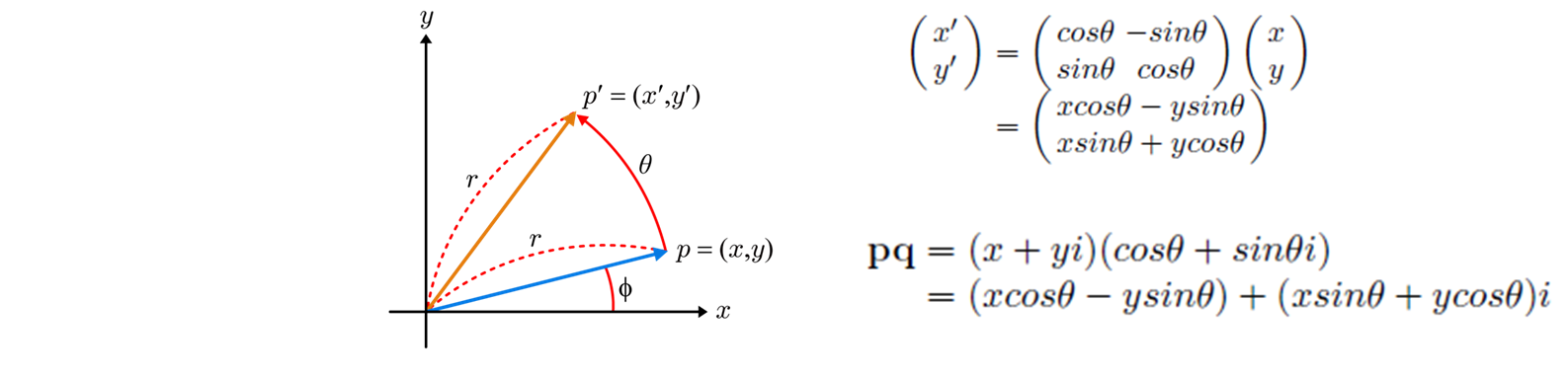
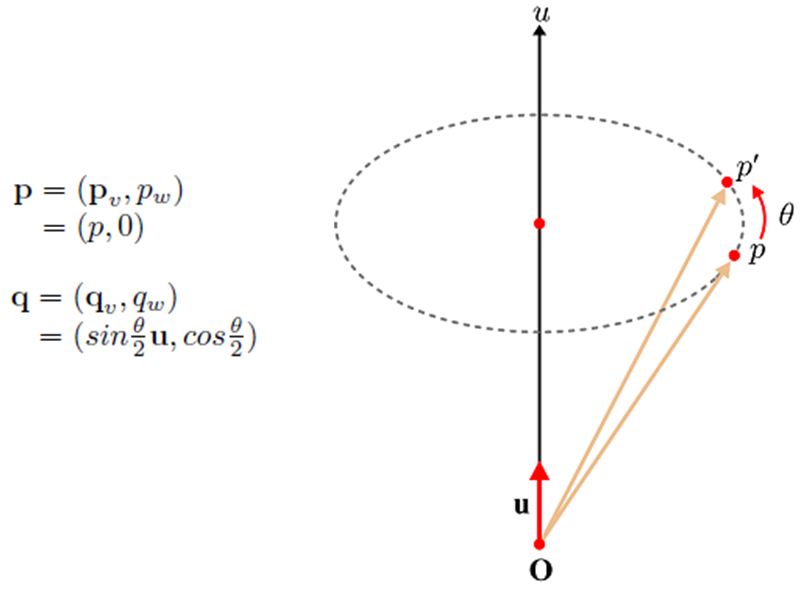
그렇다면 3D에서는 어떻게 표현될까요? 3D에서는 한 가지 허수 축이 아니라 3가지 허수 축이 있는 Quaternion을 사용합니다. 아래와 같이 u라는 축을 기준으로 θ만큼 p에서 p'으로 회전을 한다고 가정해 봅시다. 그리고 p점의 x, y, z 좌표는 Quaternion의 허수부 p_x, p_y, p_z에 들어가고, 회전을 나타내는 Quaternion은 θ와 회전축 방향으로의 단위 벡터 u를 이용해 아래와 같이 q로 표현이 됩니다. 이때 위의 2D rotation을 복소수로 나타내면 그 값들을 찾을 수 있는 거 같이 3D에서는 이 Quaternion을 이용하여 qpq*연산을 하면 그 허수부가 회전한 x', y', z'을 나타낸다고 합니다(증명 생략).
이렇게 Quaternion을 이용하여 회전할 수 있게 되면, 굳이 문제가 생길 수 있는 Euler Angle을 이용하는 것이 아니라 임의의 축을 기준으로 회전시키면 되는 것이죠. 또한 앞서 문제가 되었던 회전 변환에 대한 보간도 Quaternion은 해결할 수 있습니다.
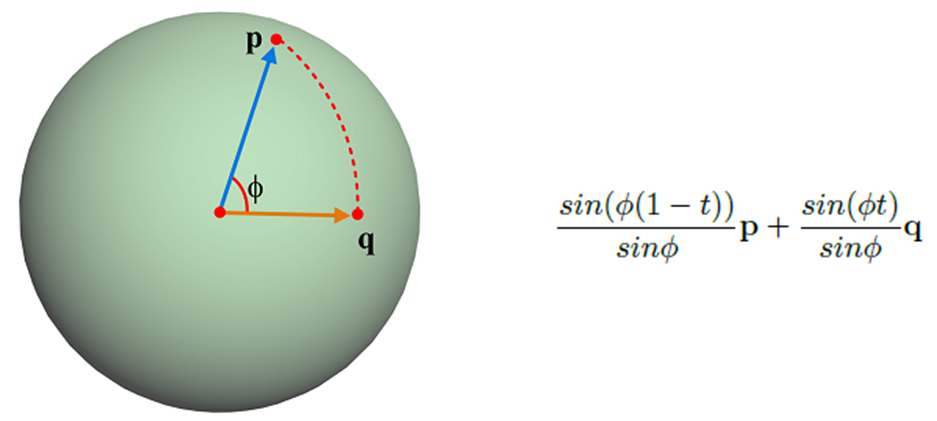
아래 그림과 같이 xyz 좌표를 아는 unit quaternion p 그리고 q를 가정했을 때, 그림 옆의 수식같이 보간이 가능합니다. 이때 ∅값은 두 quaternion의 내적을 통해 구할 수 있습니다. Unit quaternion이기 때문에 ||p||=||q||=1이 되고 따라서 ||p||*||q||*cos∅ = cos∅로 나타낼 수 있죠. 이때 각 좌표 성분 간의 곱을 합한 게 내적의 값이기도 하기 때문에 arccos을 통해 ∅를 충분히 구할 수 있죠. 따라서 아래 수식을 풀 수 있고, 보간이 가능한 것입니다. 이를 spherical linear interpolation (slerp)라고 부릅니다.
마지막으로 Quaternion 역시 Euler angle과 같이 4x4 matrix에 들어가서 표현될 수 있습니다. 아래는 Quaternion을 통한 rotation matrix를 표현한 것입니다. 이때 q는 (sin(θ/2)u, cos(θ/2))일 거 같습니다. 증명은 강의에서도 다루지 않아 저도 넘어가겠습니다. 이로써 Euler angle의 역할을 Quaternion이 다 해낼 수 있는 것이죠.
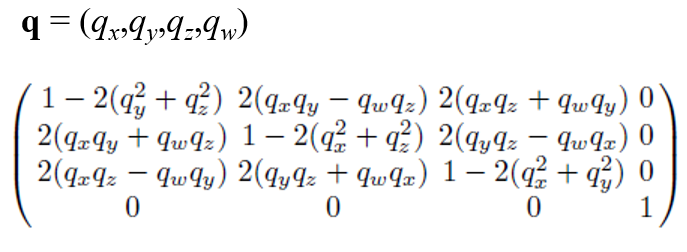
이렇게 오늘 포스팅을 통해 Quaternion을 이용한 또 다른 회전 변환 방식을 알아보았습니다.
감사합니다.
References
강의: [KUOCW] 한정현 교수님 강의
https://www.youtube.com/channel/UCfyXTCv0QlZxG1S1rteGI7A
강의 자료: 한정현 교수님 연구실 홈페이지
http://media.korea.ac.kr/books/



