이 포스팅은 [KUOCW] 한정현 교수님 강의 12장 - Screen-space Object Manipulation을 듣고 정리한 내용입니다.
선형대수학의 기초적인 지식이 필요합니다.
part1과 이어지는 포스팅입니다. 저번 포스팅에는 화면상 어떤 물체를 클릭했을 때 screen space에서 object space까지 돌아가 Object와 클릭한 좌표에서 Z 축으로 뻗어나가는 Ray와의 상호작용에 대해 알아보았습니다.
- Bounding Volume
하지만 이전 포스팅에서 같이 Ray가 모든 Object에 대해 안쪽인지 바깥쪽인지 그 거리는 얼마나 되는지 일일이 계산한다면 요구되는 computational power가 엄청날 것입니다. 따라서 이번 포스팅에서는 조금 부정확할지라도 빠르게 근사해서 풀 수 있는 방법을 소개합니다. 바로 Bounding Volume 개념입니다.
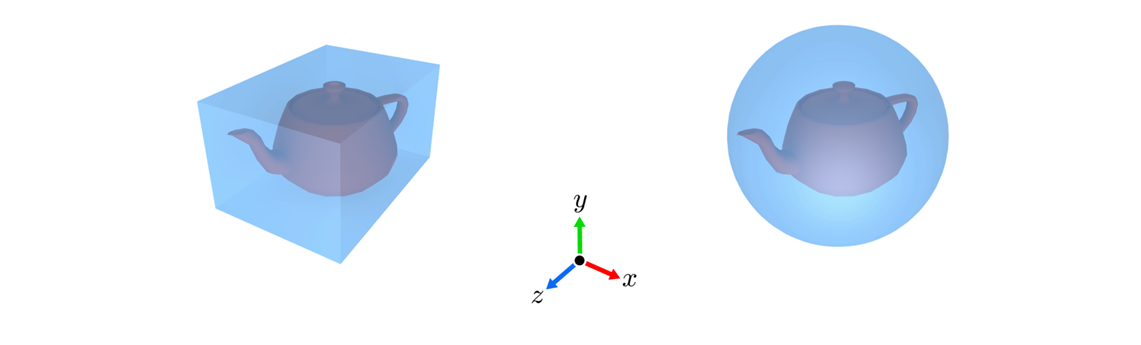
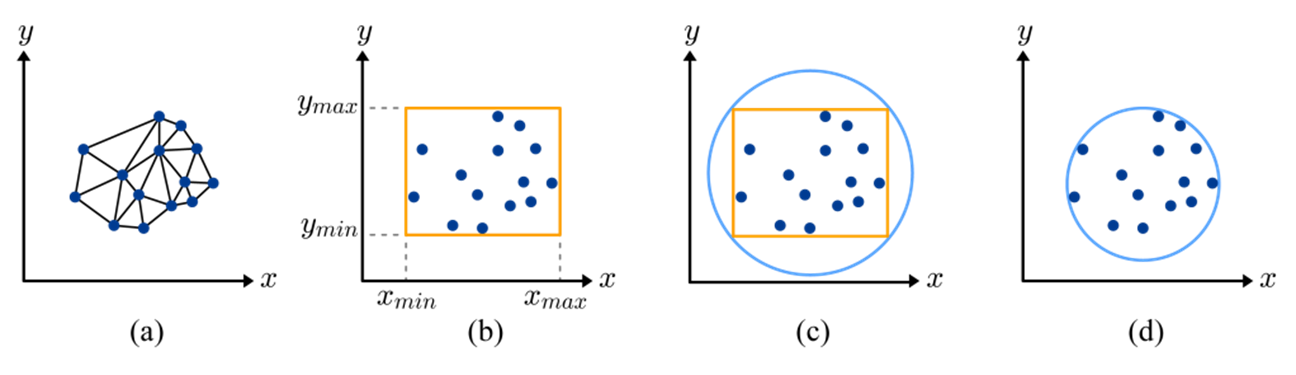
위의 그림은 Bounding Volume를 나타내고 있습니다. 어떤 Object를 둘러싼 가상의 박스를 만드는 것이죠. Object의 mesh는 그 모양이 각각 달라 각각의 좌표 정보가 요구되었습니다. 하지만 위와 같은 Bounding Volume은 최소한의 파라미터만 요구되죠. Box는 X, Y, Z 축으로의 min/max가 Sphere는 중심점 좌표와 반지름으로 그 Volume을 충분히 계산할 수 있죠. xy-plane에서 설명하면 아래와 같이 나타낼 수 있습니다. 오른쪽 (d)처럼 계산될 수 있는 것은 계산 기하학을 통한 최적화라고 합니다. 역시 수학이 중요하네요
Bounding Volume을 Sphere로 가정하면, ray인 s+td을 이용하여 아래 수식과 같이 구의 방정식의 x, y, z 변수를 치환할 수 있죠. 이렇게 식을 풀어내면 구의 중심 C와 반지름 r 그리고 ray의 starting point s와 방향벡터 d는 모두 아는 정보이기 주어진 정보이기 때문에, t에 대한 2차 방정식이 나오게 됩니다. 그리고 근의 공식을 통해 t의 값을 구할 수 있죠. 이렇게 되면 t가 두 개의 근을 가질 때는 Ojbect를 통과할 때(작은 t값을 선택합니다), 중근을 가질 때는 접할 때, 허근을 가질 때는 접하지 않을 때로 판단할 수 있게 되는 것이죠.
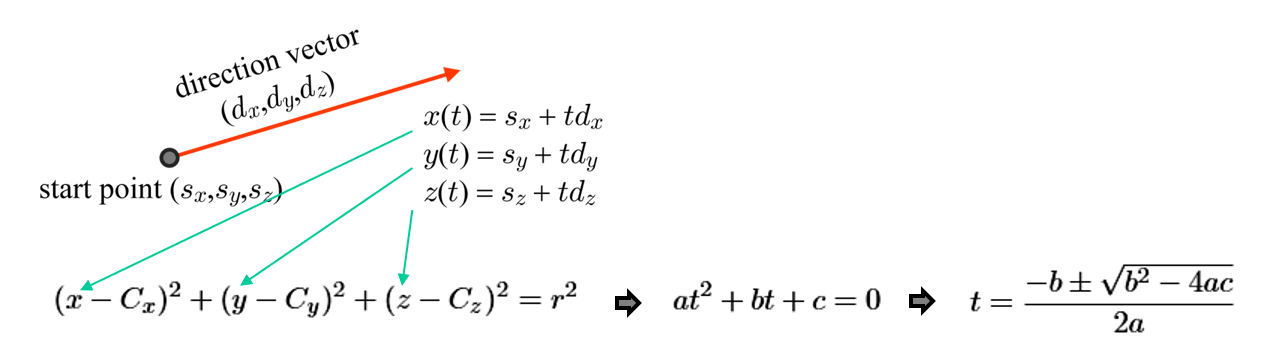
하지만 이 방법을 사용하면 보시는 것과 같이 비교적 간단한 연산을 통해 Bounding Volume Sphere와 ray의 교점을 알아낼 수 있지만, 아래 왼쪽 그림과 같이 실제 Object가 아닌 영역도 포함하기 때문에 판단에 오류가 있을 수 있음을 알 수 있죠. 따라서 이 방법은 통과하지 않는 물체를 빠르게 가려내는 데 사용한다고 합니다. Bounding Volume을 통과하지 않지만 Object는 통과하는 경우는 절대 없기 때문이죠.

- Object Rotation and Arcball
지금까지는 화면을 클릭했을 때, 해당 좌표의 물체가 어떻게 적절하게 선택되는지 알아보았습니다. 이제는 그 물체를 드래그했을 때 회전하는 상호작용에 대해 알아보겠습니다. 우선, 아래 그림은 화면을 좌에서 우로 드래그했을 때 주전자가 돌아가는 것을 나타냅니다. 그리고 화면에서 얻을 수 있는 정보는 오른쪽 그림같이 2D 화면상 pi에서 pi+1... pi+n 같이 연속적인 좌표를 얻을 수 있죠. 이 좌표를 어떤 방식으로 처리해서 회전할 수 있을까요?
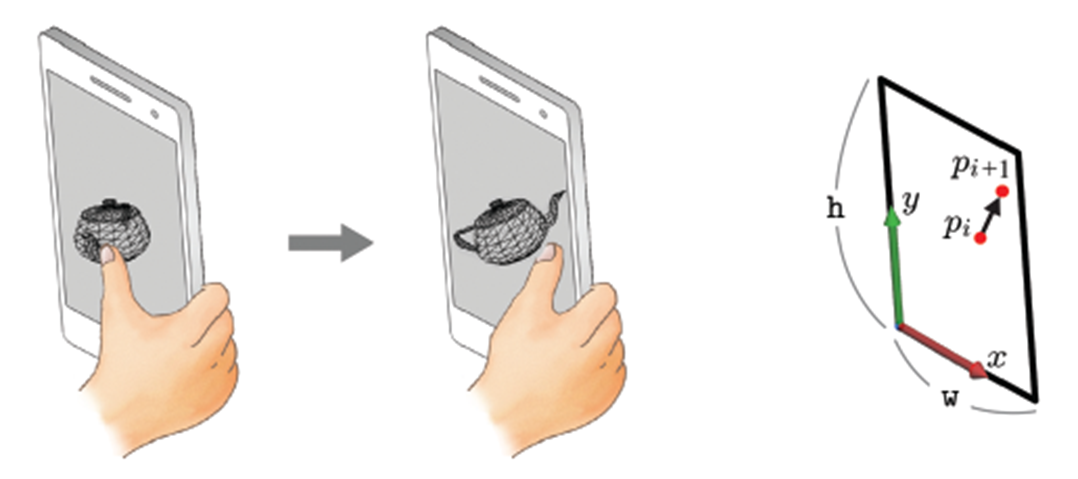
여기서 Arcball이라는 개념이 등장합니다. Arcball은 가상의 구로 X, Y 각 [-1,1] 범위의 정육면체 안에 존재하죠. 화살표 아래 x', y'를 나타내는 수식은 가로세로 각각 w, h인 스크린 좌표가 Arcball이 존재하는 정육면체에 어떻게 맵핑되는지를 나타냅니다. 이때 Arcball 공간상에서 z 축으로는 +1인 지점에 맵핑이 되죠.
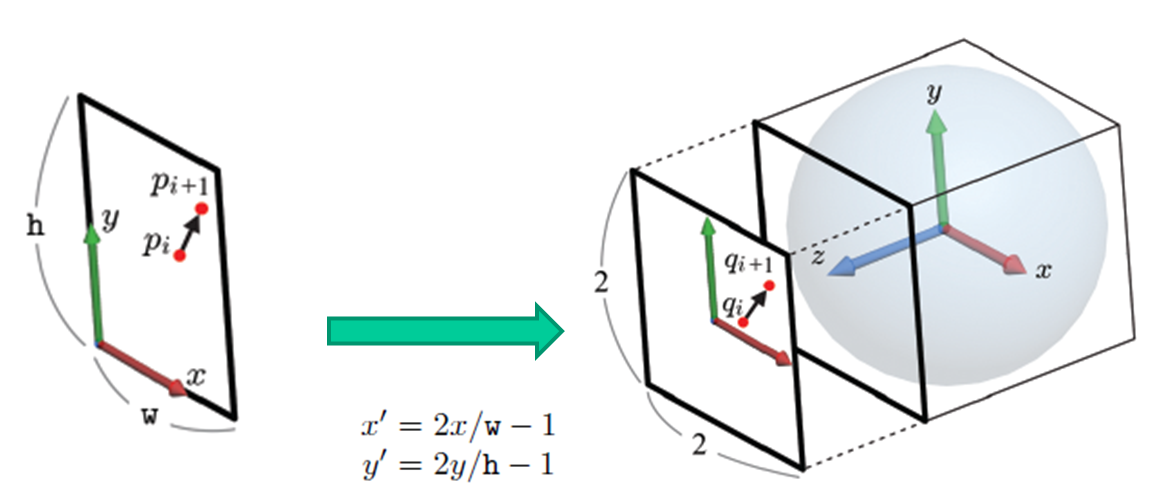
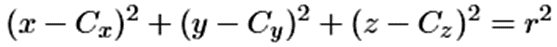
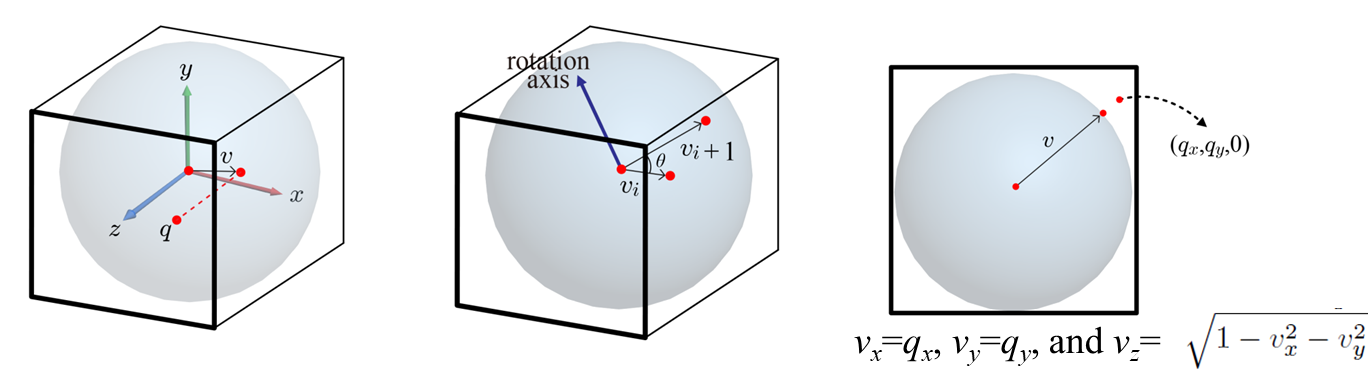
이제 Arcball 공간상에 찍힌 좌표를 통해 Arcball의 표면에 projection을 시킵니다. z좌표만 모르기 때문에 구의 방정식에 x, y를 대입해서 풀어낼 수 있죠. 아래 그림처럼 알아낸 Arcball의 표면 연속된 좌표 v_i와 v_i+1 두 점의 좌표를 외적 하여 rotation axis 또한 구해낼 수 있습니다. 또한 단위 구 위의 점이므로 두 점 모두 단위 벡터입니다. 따라서 내적을 통해서 두 점 사이의 각도 또한 쉽게 알 수 있죠. 또한 오른쪽 그림처럼 Arcball 표면상에 projection 시킬 수 없는 경우는 z좌표를 0으로 하는 xy-plane상에 가장 가까운 Arcball의 표면에 그 아래 수식을 이용해 위치시킵니다.
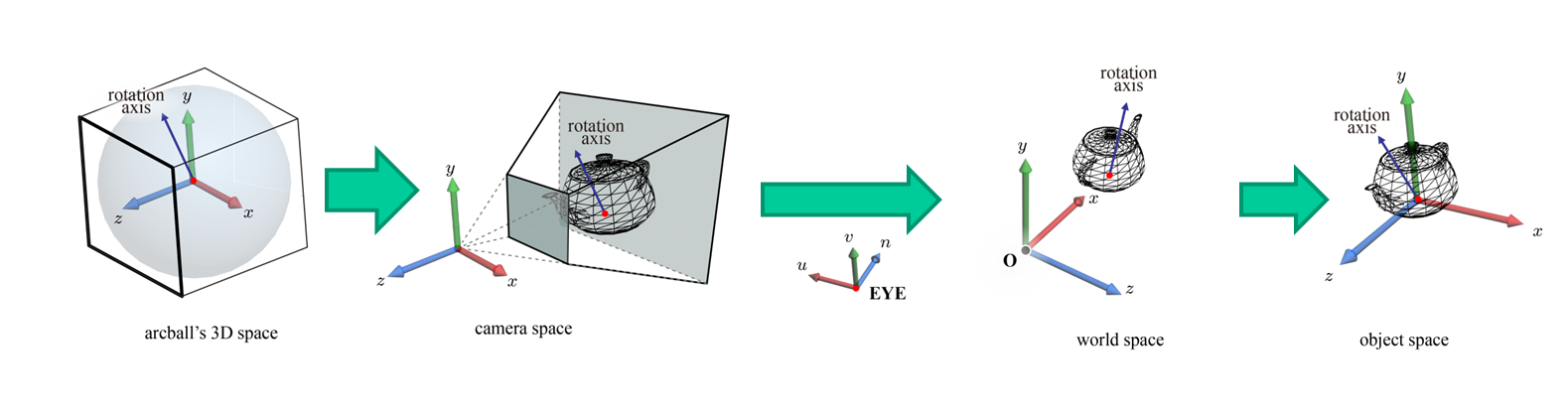
이렇게 Arcball을 이용해 회전축과 각도 모두 구할 수 있다는 것을 알았습니다. 하지만 정작 회전해야 할 object가 아직 언급이 없죠. 그래픽스에서는 Arcball에서 구한 회전축을 camera 공간상에 위치시키는 방법을 사용합니다. 이렇게 위치시킨 회전축 또한 역변환을 통해 object space로 변환하여 object space상 변환된 회전축을 기준으로 구한 각도만큼 회전을 시키는 것이죠. 이렇게 2D 화면상 pi에서 pi+1... pi+n를 연속되게 계산하면 화면을 드래그했을 때, 물체의 회전을 만들 수 있게 되는 것이죠. (회전축과 각도가 있으면 회전 변환이 가능하다는 것은 Quaternion포스팅 참고 바랍니다)
이렇게 화면에 해당 Object가 어떻게 선택되는지 또 드래그했을 때 어떻게 회전하게 될 수 있는지까지 알아보았습니다. 배우면서 느낀 점은 많은 계산이 실시간으로 이루어지고 있다니, 우리가 가진 장비의 성능에 다시금 놀라게 되는 거 같습니다.
저 개인적인 생각으로는 회전축을 적용시킬 때 camera space가 아닌 clip space로 적용해야 하지 않나도 싶습니다. 지금 구한 두 점 간의 계산은 clip space상에서 이루어졌다고 보는데, View Frustum에서 clip space상으로 변환할 때 왜곡을 수정해주지 않고 구한 회전축을 camera space에 바로 적용할 수 있냐에 대해 의문이 조금 듭니다. 혹시 읽으시는 분들의 생각은 어떠신가요?
감사합니다.
References
강의: [KUOCW] 한정현 교수님 강의
https://www.youtube.com/channel/UCfyXTCv0QlZxG1S1rteGI7A
강의 자료: 한정현 교수님 연구실 홈페이지
http://media.korea.ac.kr/books/
'컴퓨터 그래픽스' 카테고리의 다른 글
| 컴퓨터 그래픽스 - Normal Mapping([KUOCW] 한정현 교수님 강의) (0) | 2022.02.06 |
|---|---|
| 컴퓨터 그래픽스 - Character Animation([KUOCW] 한정현 교수님 강의) (0) | 2022.02.04 |
| 컴퓨터 그래픽스 - Screen-space Object Manipulation part 1. Object Picking ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.21 |
| 컴퓨터 그래픽스 - Quaternion ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.20 |
| 컴퓨터 그래픽스 기초 - Output Merger ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.20 |



