이 포스팅은 [KUOCW] 한정현 교수님 강의 12장 - Screen-space Object Manipulation을 듣고 정리한 내용입니다.
선형대수학의 기초적인 지식이 필요합니다.
오늘은 Screen-space상의 Object가 어떻게 상호작용이 되는지 살펴보겠습니다.
- Object Picking
게임에서 화면 상에 어떤 Object를 클릭했을 때, 그 Object가 선택되는 것을 아실 겁니다. 이때 사용자가 클릭한 것은 지금 보고 있는 모니터, Screen space에서 클릭을 한 것이죠. 하지만 이전 포스팅을 통해 Rendering pipeline을 숙지하셨다면, Screen space에는 Object라는 개념이 없다는 것을 아실 겁니다. 단지 개별적인 pixel값만 존재할 뿐이죠.
어떠한 방법으로 클릭을 통해 해당 object와 상호작용 할 수 있을까요? 가장 먼저 해야할 일은 클릭한 지점 (x, y,0)에서 z 축으로 뻗는 ray-object(direction vector) 벡터를 만드는 것입니다. 이는 같은 선상의 z 축을 통과하죠. 이 ray-object가 아래 오른쪽 그림과 같이 처음 맞닿는 object에 닿으면 그 object가 클릭했을 때 골라지는 object임을 직관적으로 우리는 알 수 있죠.
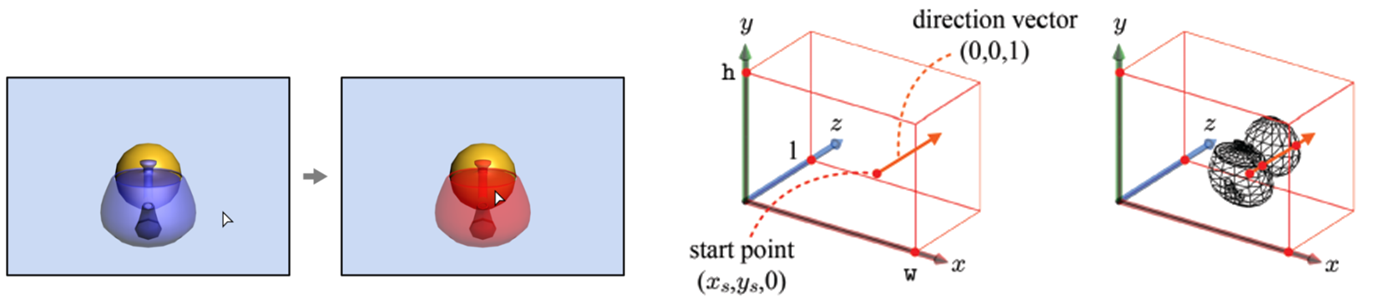
하지만 앞서 말한대로 컴퓨터는 screen space에서 직관적으로 클릭한 좌표가 어떤 object가 해당되는지 알지 못합니다. 따라서, object와 상호작용 할 수 있는 공간으로 direction vector를 옮겨야 하죠. 그러한 공간은 바로 object space입니다. 그럼 지금까지 해왔던 변환의 역변환을 통해 screen space에서 object space까지 가야 할 것입니다. 먼저 아래 그림과 수식을 통해 camera space부터 screen space까지의 변환을 확인할 수 있습니다(n=1로 가정). camera space에서 projection transform을 통해 clip space로, clip space에서 viewport transform으로 screen space로 변환하였죠.
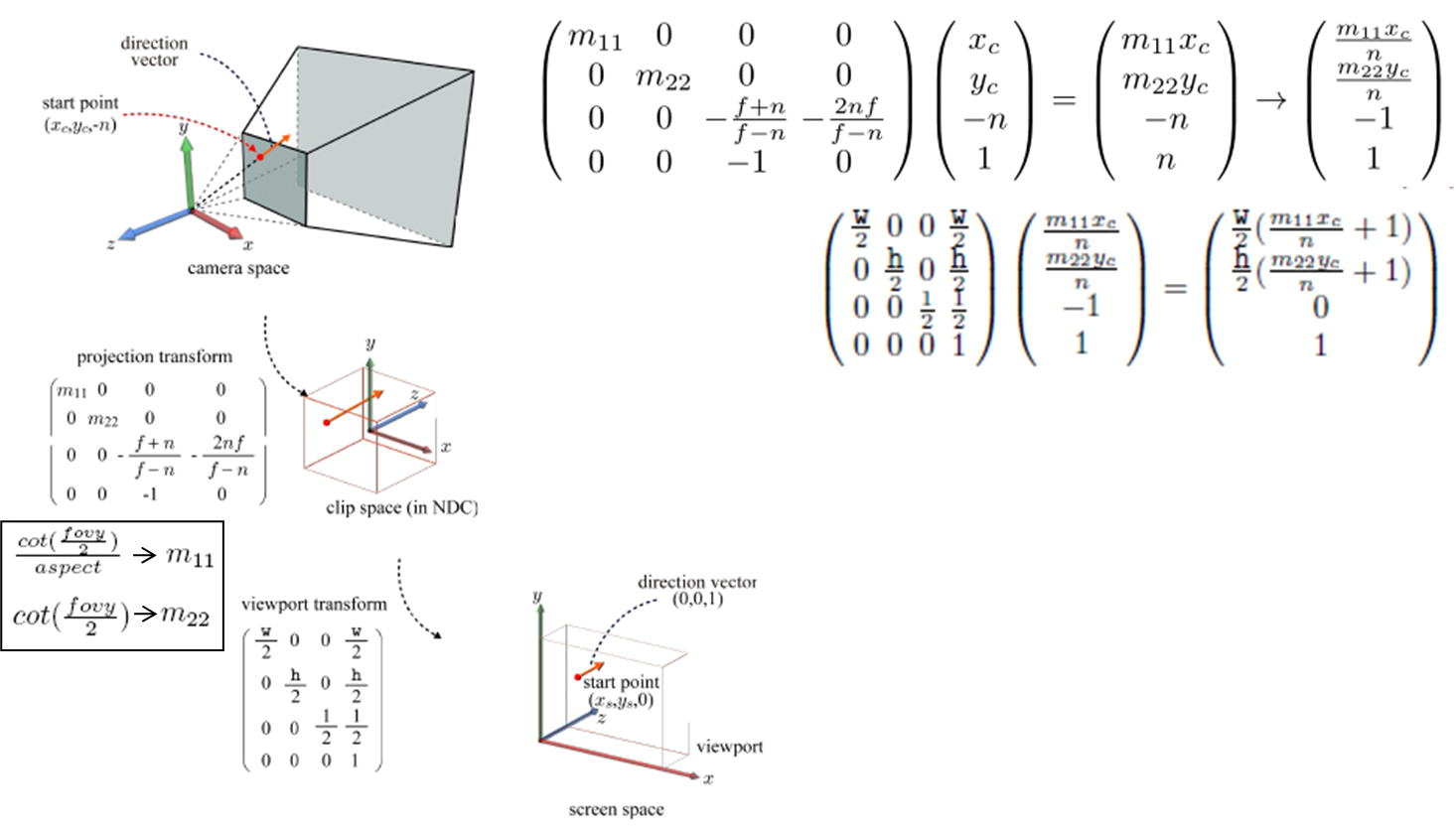
위의 식을 풀어 screen space상의 좌표를 camera space상의 좌표로 계산할 수 있습니다. direction vector 또한 같은 원리로 camera space상의 벡터로 아래와 같이 나타낼 수 있죠.

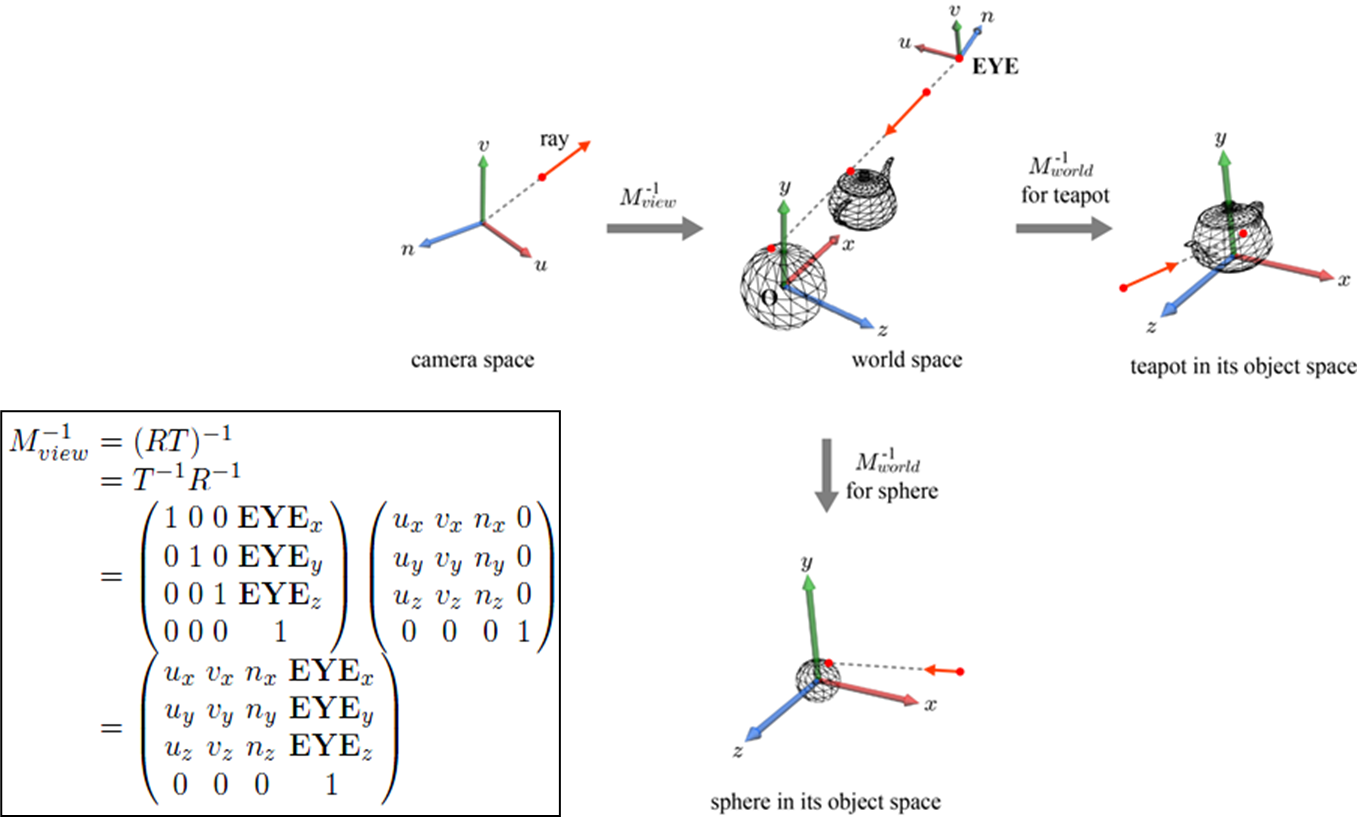
이렇게 camera space까지 오게 되었습니다. 하지만 최종 목적지인 object space는 world transform을 이용해 world space로, world space에서는 view transform을 통해 camera space로 왔었죠. 따라서, 이 두 변환에 대한 역변환 또한 요구됩니다.
view transform은 앞서 설명한것과 같이 rotation과 translation을 통해 이루어지므로 아래 수식과 같이 그 역변환을 표현할 수 있습니다. 또한 각 object들은 world space로 오기 위해 각각의 world transform matrix를 통해 연산되었습니다. 따라서 각각의 world transform 또한 affine transform이기 때문에 이전에 언급한 대로 비교적 쉽게 그 역변환을 구할 수 있죠. 이런 방식을 통해 최종적으로 screen space에서 object space까지 올 수 있음을 확인하였습니다. direction vector도 같이 말이죠.
이렇게 object space에서의 direction vector(ray)가 object의 어떤 삼각형 mesh에 정확히 찍혀지는지 어떻게 알 수 있을까요? 혹은 찍히는지 안 찍히는지 여부를 말입니다. 이를 알기 위해서 weights (u,v,w)라는 개념을 사용합니다.
아래 정의를 보면 아시다시피 (u,v,w)은 삼각형 mesh위에 찍힌 점 p를 기준으로 한 삼각형 넓이를 얼마나 차지하고 있냐를 나타냅니다. 이를 이용해 p=ua+vb+wc같이 벡터의 합으로 나타낼 수 있다고 하네요. 이때 (u, v, w) 3 원소의 합은 1 이므로 점 p를 화살표 왼쪽과 같이도 표현 가능하죠.

우리는 ray를 start point와 단위 벡터 d를 통해 s + td로 나타낼 수 있습니다. 따라서 점 p = s+td = ua+vb+(1-u-v)로 나타낼 수 있죠. 이때, d와 mesh의 각 꼭짓점 a, b, c는 각각 x, y, z 성분을 가지고 있습니다. 따라서 아래와 같이 수식을 정리할 수 있죠. 이때 꼭짓점 a, b, c는 그림에서 A, B, C로 표기됩니다.
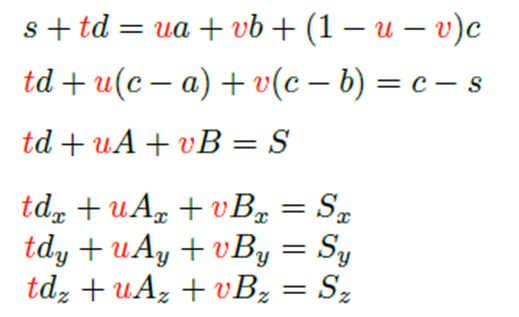
맨 마지막 3줄을 보시면 t,u,vt, u, v 3가지 미지수와 3가지 식으로 정리되었음을 확인할 수 있습니다. 이때 d, A, B, S는 모두 아는 값입니다. 따라서 연립방정식을 통해 t, u, v 3가지 미지수를 찾을 수 있죠. 더 간단하게 Cramer's rule를 이용하여 아래 풀이와 같이 각 미지수를 계산할 수 있습니다.
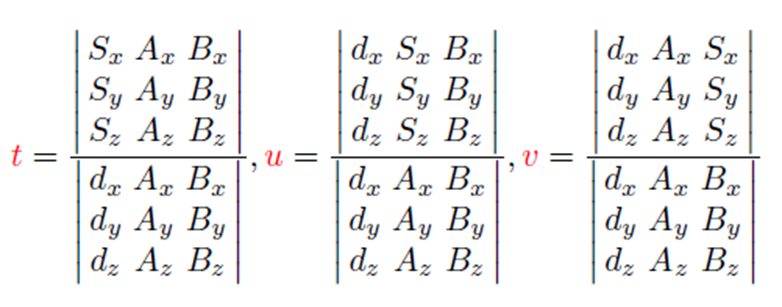
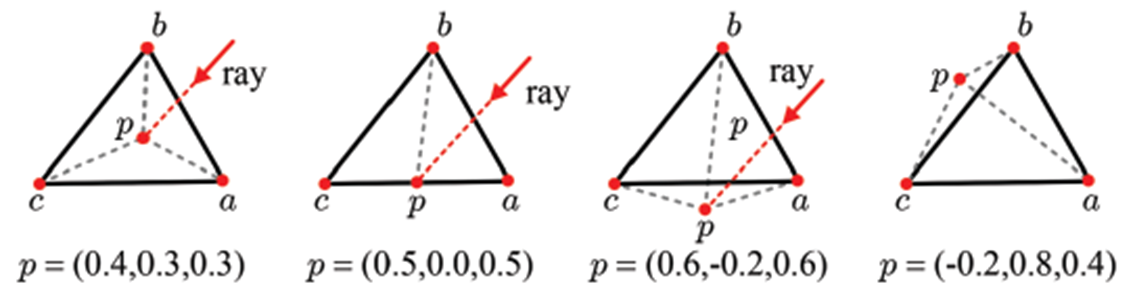
이렇게 미지수를 구했다면, 이 값들을 이용해서 해당 삼각형 mesh에 ray가 통과하는지 안하는지 알 수가 있습니다. 바로 u ≥ 0,v ≥ 0, and u+v ≤ 1 이 만족해야 해당 mesh를 통과한다고 볼 수 있는 것이죠. 아래 그림에서는 ray에 의한 점 p가 mesh의 안에 찍히는지 밖에 찍히는지를 보이고 있습니다. 이때 점선과 mesh의 모서리와 점 p를 이어 만든 삼각형이 mesh 안에서만 존재하면 u ≥ 0,v ≥ 0 and u+v ≤ 1이 만족하는 것이고 그렇지 않으면 만족하지 않습니다. 이렇게 해당 삼각형 mesh에 ray가 통과하는지 안 하는지 계산이 될 수 있는 것이죠.
마지막으로, 입체적인 object는 ray가 object 두 부분을 지날 수도 있습니다. 아래 그림과 같이 말이죠. 이때는 ray가 닿는 지점 p = s + td 에서 t가 작은 지점의 mesh를 선택합니다. 이는 ray가 가장 먼저 닿은 지점으로 보는 것이죠. 또한 t의 값은 위에서 알 수 있음을 보였습니다. 이런 방식을 통해 screen space에서 클릭했을 때 어떤 object가 선택돼야 하는지 알 수 있게 되는 것이죠.

다음은 좀더 위의 방법을 빠르게 근사하는 방법과 회전 상호작용에 대해 알아보겠습니다.
감사합니다.
References
강의: [KUOCW] 한정현 교수님 강의
https://www.youtube.com/channel/UCfyXTCv0QlZxG1S1rteGI7A
강의 자료: 한정현 교수님 연구실 홈페이지
http://media.korea.ac.kr/books/
'컴퓨터 그래픽스' 카테고리의 다른 글
| 컴퓨터 그래픽스 - Character Animation([KUOCW] 한정현 교수님 강의) (0) | 2022.02.04 |
|---|---|
| 컴퓨터 그래픽스 - Screen-space Object Manipulation part 2. Bounding Volume and ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.21 |
| 컴퓨터 그래픽스 - Quaternion ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.20 |
| 컴퓨터 그래픽스 기초 - Output Merger ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.20 |
| 컴퓨터 그래픽스 기초 - Fragment Shader part 2. Phong Lighting ([KUOCW] 한정현 교수님 강의) (0) | 2022.01.19 |



