https://wikibook.co.kr/reinforcement-learning/
파이썬과 케라스로 배우는 강화학습: 내 손으로 직접 구현하는 게임 인공지능
“강화학습을 쉽게 이해하고 코드로 구현하기” 강화학습의 기초부터 최근 알고리즘까지 친절하게 설명한다! ‘알파고’로부터 받은 신선한 충격으로 많은 사람들이 강화학습에 관심을 가지
wikibook.co.kr
해당 포스팅은 위의 책을 보고 정리한 내용입니다.
상태(S_t): t 시점에서 에이전트가 인식하고 있는 자신의 상황.
행동(A_t): t 시점에서 에이전트가 인식하고 있는 상황에서 취할 수 있는 행동.
보상 함수: 에이전트가 어떤 행동을 했을 때, 얻을 수 있는 보상, 기댓값
상태 변환 확률: S_t에서 A_t했을때 다음 상태s 일 확률.
할인율: 나중에 받을수록 보상을 줄이는 요소(factor)
이전 글에서는 MDP의 각 성분들을 위와 같이 알아봤습니다.
이번 포스팅에는 정책, 가치 함수 그리고 큐 함수 개념을 설명해보려 합니다.
- 정책(Policy)
정책이란, 모든 상태에서 에이전트가 할 행동입니다.
아래 그림과 같이 시작점에서 도착점까지는 화살표를 통해 최단 거리로 갈 수 있습니다.
이렇게 되면 그리드월드에서의 최적을 찾은걸까요?
시작점 S_1 = (1,1)에서 화살표만 따라가면 도착점에 최단거리로 갈 수있으니까요.
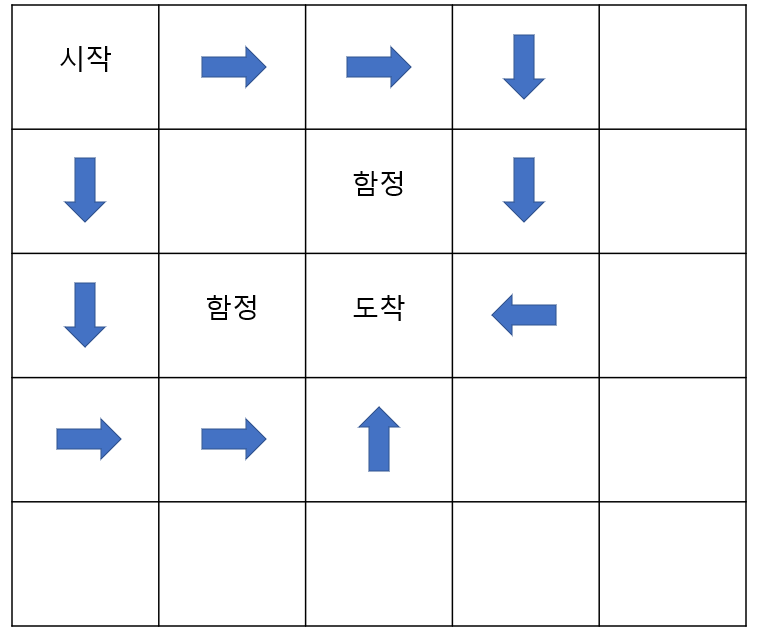
하지만 상태 변환 확률에서 언급했듯, 어떤 상태 S_t에서 A_t를 통해 S_t+1로 가는 것은 정해진 것이 아니라,
확률적으로 이루어집니다.(예시: 빙판길에서 미끄러짐, 바람이 불어 밀림)
따라서, 이에 맞게 정책또한 확률로써 아래와 같이 표현됨을 우리는 알 수 있습니다.
조건부 확률로 나타내지는데, 어떤 상태 s 에서 행동 a를 취하는 것은 확률 p로 표현되는 것을 확인 할 수 있습니다.
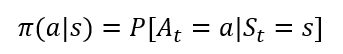
위의 그림의 화살표는 에이전트가 움직이고 싶은 방향으로 100% 움직일 수 있다는 전제하의 그림입니다. 만약 굉장히 미끄러운 빙판이라면 반대 방향으로 미끄러지지 않기 위해 움직여야 할 수도 있고, 매우 기울어진 상태라면 앞으로가는것이 오른쪽이나 왼쪽으로 움직이는 것이 될 수 있습니다. 에이전트는 이런 환경에 적응(학습)하고 보상이 최대가 되도록 정책을(화살표 방향)을 업데이트(학습)할것입니다.
- (re)할인율 𝛾
가치 함수 이전에 할인율 𝛾를 다시 보겠습니다. 왜 아래와 같이 빨간 선을 따라 시작점에서 도착점까지 가면 최적의 경로가 안되는 걸까요? 파란 화살표가 아닌 빨간 선을 따라 도착해도 보상을 받을 수 있다면, 실제로 차이가 없습니다. 하지만 사람이라면 저 루트가 최적이 아니라 돌아감을 알 수 있죠. 이 개념을 할인율로 에이전트에게 알려 줄 수 있습니다. 할인율이 없다면 도착 시 보상 R을 받겠지만, 할인율을 적용하면 파란 화살표를 따라가면 6칸만에 이동하기 때문에 𝛾^6*R 보상을, 빨간 선을 따라가면 𝛾^18*R의 보상을 받습니다. 이때, γ∈[0,1]이기 때문에 더 많은 칸을 이동할 수록 보상이 작아집니다.
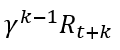
책에서 보상을 설명할때(pp.44-45), 바로 아래 수식과 같이 설명하는데, 그리드 월드에서는 도착점 말고는 다른 보상이 없기 때문에, 그 아래 수식같이 구성 될 것입니다. 반환값 G_t는 어떤 시점에서 부터 받은 보상을 계산할때 사용됩니다. 이를 이용해 어떤 시점에서의 가치(보상의 정도)를 계산 할 수 있는 것이죠.
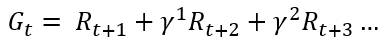
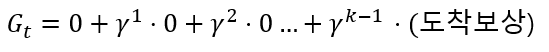
이 부분은 다른 포스팅 혹은 강의도 참고하시는게 좋을거 같습니다.
한 스텝씩 설명해주는 포스팅이나 유튜브 강의가 많이 있습니다.
- 상태 가치 함수
돌아와서, 보상이 최대가 되는 최적 정책을 찾으려면, 컴퓨터인 에이전트에게 어떤 상태 S_t에서 어떤 행동 A_t가 가치있는 행동인지를 알려줘야 합니다. 강화학습에서는 가치 함수 v(s)를 이용해 이 문제를 해결합니다.
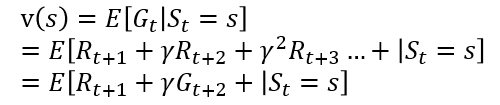
여기서 정책을 고려하게 된다면, 아래와 같은 수식으로 표현됩니다. 이때, G_t+2가 v(S_t+1)로 표현됨을 알 수 있습니다.
수식을 보시면 상태 s일때, 앞으로 얻게되는 보상에 대한 기댓값임을 볼 수 있습니다.
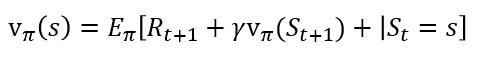
- 행동 가치 함수(Q-function)
위를 통해 어떤 상태에서 받을 수 있는 보상을 수식화 하였습니다. 다음으로는, Q-function이라 불리는 행동 가치 함수입니다. 어떤 상태에서 어떤 행동을 취했을 때, 얻게되는 보상에 대한 기댓값 이라고 이해하시면 되고, q_π(s,a)로 나타내집니다.
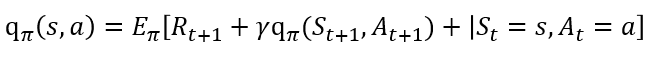
또한 행동가치함수와 상태가치함수 사이는 다음과 같이 표현 할 수 있습니다. 조금 복잡해 보이지만, 차분히 보시면, 어떤 상태 s 에서 모든 행동으로부터 오는 보상(q_π(s,a))과 그 행동을 할 확률(π(a|s))의 곱을 합(Σ)을 더한 것 뿐이라는 것을 알 수 있습니다.
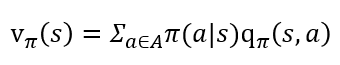
- 벨만 방정식(Bellmam Equation)
벨만이라는 이름에 굉장한 수학적 개념이 있는듯해 멈칫하셨을 수도 있는데, 책에서는 현재상태의 가치함수와 다음 상태의 가치함수의 관계식이 벨만 방정식이라고 설명합니다. 이미 위의 수식이 우리가 사용할 벨만 방정식이라고 이해하셔도 좋을거 같습니다. 단지 이름이 붙었을 뿐입니다! 책에서도 위에 언급된 상태 가치 함수를 아래 벨만 기대 방정식으로 그대로 쓰는 것을 확인 할 수 있습니다.
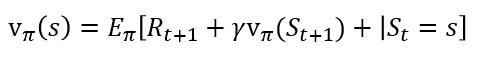
이 벨만 기대 방정식을 통해 최적의 정책을 찾는 것(최고의 보상을 받는 것)인데요. 이는 어떤 상태에서 최적의 행동 a를 하는 것으로 이해할 수도 있습니다. 따라서 행동가치함수, 상태가치함수 모두 최적을 선택해야하는 것이죠. (두 함수는위에 언급했듯 관계가 있습니다.) 하지만 처음부터 한번에 찾는 것은 쉽지 않습니다. 에이전트는 학습시 자신이 경험(학습) 기반으로 값을 업데이트하며, 최적을 찾아갑니다. 아래 두 수식은 현재의 정책을 통해, 최적의 q와 v를 선택하는 것이고, 가장 아래는 현재의 정책이란 가장 q값이 큰것을 취해 행동 a 를 한다는 의미입니다.
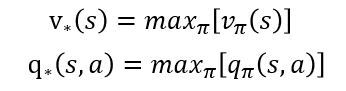
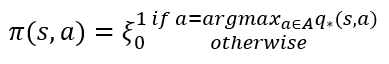
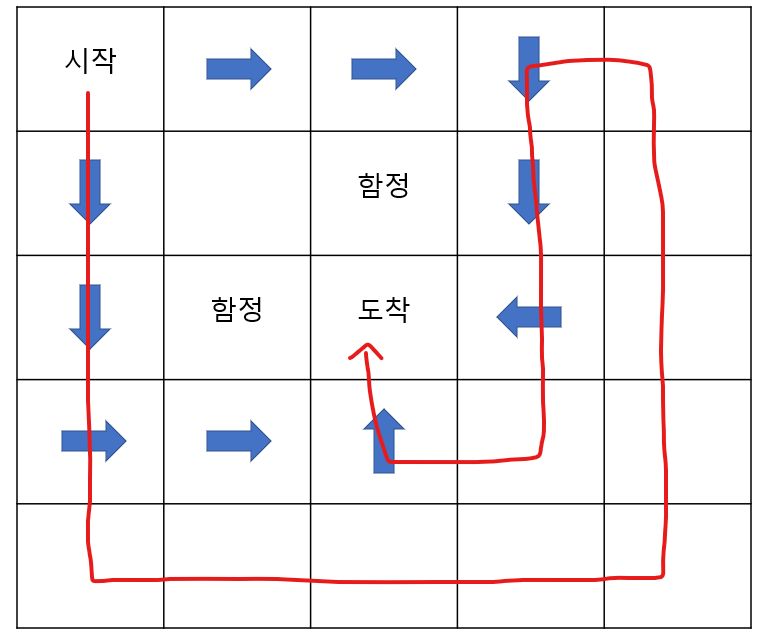
위의 수식들은 모두 "현재" 에이전트가 아는 정보를 기반으로 이루어진다는 것을 아셔야 합니다. 다시 아래 그림을 가지고 설명 하겠습니다. 에이전트는 처음 시작점에 놓였을 때, 아무 정보 없이(다음 칸에 무엇이 있는지 모르는 상태)로 맵을 떠돌아 다닐 것입니다. 이 때, 모든 행동은 uniform한 분포일 것입니다. 어디로 가든 기댓 값은 0일테니까요.

하지만, 빨간 선으로 첫 시도(에피소드)가 끝나면 그 위에서 언급한 수식들을 통해 각 상태와 행동에 대한 보상을 업데이트 할 것입니다. 그렇다면, 다음 에피소드에는 에이전트 입장에서 빨간 선을 따라 가는 방향이 가장 최적의 선택이 되는 것이겠죠. (이는 함정으로 가지 않았다는 가정하에 말씀드렸습니다, 만약 함정에 가게되었으면, 보상이 음수로 업데이트되어 빨간 선과 다른 방향으로 최적이 설정될 것입니다.) 하지만 이렇게 되면 빨간 선으로만 가는 것이 아니냐고 생각 하실 수 있는데, 이는 test시에 그렇게 이루어지지, train(학습)시에는 또 다양한 방법론에 의해 다양한 루트를 탐험 또는 실험 하게 됩니다. 이는 나중에 설명 드릴 예정입니다.
이제 이 부분이 지금까지의 총체입니다. 행동가치함수 v는 아래처럼 기댓값을 풀어 설명할 수 있습니다. 이때 P로 표현된 상태 변환 확률이 1로 가정하면 보시는 것처럼 되는 것을 확인 할 수 있습니다. 그리고 한번의 에피소드가 끝나면, 그 아래 업데이트라고 적힌 수식같이 행동가치함수가 최신화되고, 그에 따른 정책이 바뀌게될 것입니다. 행동에 따라 얻게되는 보상이 바뀌었으니, 어떻게 행동할지도 당연히 바뀌는 것이지요.
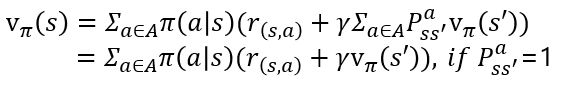
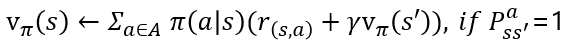
이 일련의 업데이트 수많은 학습 과정을 통해 v 그리고 v와 관계된 q도 같이 업데이트가 되면 업데이트 수식의 화살표는 등호로 바뀌게 될것입니다. 저는 수렴했다고 이해했습니다. 그렇게 된다면 최적의 함수들을 찾게 된 것입니다. 이제 찾은 함수를 기반으로 구성한 최적의 정책으로 행동한다면, 최적의 보상을 받을 수 있을 것입니다. 따라서, 그리드 월드에서는 최단거리로 도착하게 되는 것이죠. 이것은 아래와 수식과 같이 벨만 최적 방정식이 표현될 것입니다. 이 수식들이 기댓값으로 표현된 이유는 상태 변환 확률을 고려하기 때문입니다.
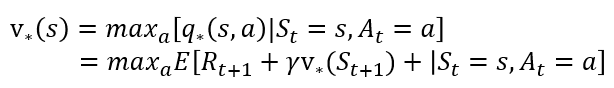
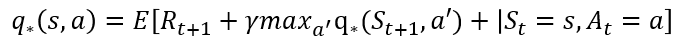
이렇게, 최적의 가치를 찾기 위해 표현되는 수식을 알아보았습니다. 그리드 월드 기준으로 다음과 같은 수식을 통해서, 에이전트는 최고의 보상을 받기 위해 함정은 피하고, 목표에 도달할 것이며, 가장 할인율의 영향이 적게 하기위해 가장 짧은 루트에 가치를 둘 것입니다. 이는 상태가치함수와 행동가치함수를 통해 표현되고, 마지막에는 이 지표를 따라 각 상 태 s에 따라 가장 많은 보상이 기대되는 행동 a를 취할 것임을 알 수 있습니다.
이번 포스팅에서 나온 개념들을 정리하자면 아래와 같습니다.
- 상태 가치 함수: 현재 정책에 따라 어떤 상태에서 얻을 수 있는 보상의 기댓값
- 행동 가치 함수(Q-function): 현재 정책에 따라 어떤 행동을 통해서 얻을 수 있는 보상의 기댓값
- 벨만 방정식: 강화학습에서 현재상태의 가치함수와 다음 상태의 가치함수의 관계식
- 벨만 기대 방정식: 특정(현재) 정책을 따라갔을 때 가치함수 사이의 관계식
- 벨만 최적 방정식: 최적의 정책을 따라갔을 때 가치함수 사이의 관계식
감사합니다.
'강화 학습' 카테고리의 다른 글
| 강화 학습 기본 - ε-탐욕 정책(ε-greedy Policy) 그리고 ε-decay (0) | 2022.01.07 |
|---|---|
| 강화 학습 기본 - 몬테카를로 근사(Monte Carlo Approximation) (0) | 2022.01.06 |
| 강화 학습 기초 - 다이나믹 프로그래밍의 한계(Limitation of Dynamic programming) (2) | 2022.01.05 |
| 강화 학습 기초 - MDP(마르코프 결정 과정, Markov Decision Process) (2) | 2022.01.04 |
| 강화 학습 개요 (2) | 2022.01.04 |



