남겨놓는 Diffusion 기본 논문들 간단 메모
Reference:
https://cvpr2022-tutorial-diffusion-models.github.io/
https://www.youtube.com/watch?v=uFoGaIVHfoE
1. DDPM:
1. 이미지(t=0)에 t=n step의 가우시안 노이즈를 미세하게 계속 더하면 노이즈가 될 것
2. 그럼 이러한 노이즈에서 노이즈를 걷어내면 이미지가 될 것
3. t step에서 더해진 노이즈를 예측가능하면 t-1번째 이미지를 만들 수 있음.
4. 이를 통해 t=n에서 t=0까지 도달하면 이미지가 될 것.



2. DDIM
1. 기존 Markov Chain으로 정의됨. DDPM은 '반드시' 순서대로 만들어야함
2. Non-Markov가 되도록 DDIM으로 만든 것
3. 순차적이지 않아도 됨 (점프 가능) X_0에서 X_t로
4. 빠른 샘플링과 randomness 조절이 가능

3. Score-based model
score-based와 diffusion의 관계.
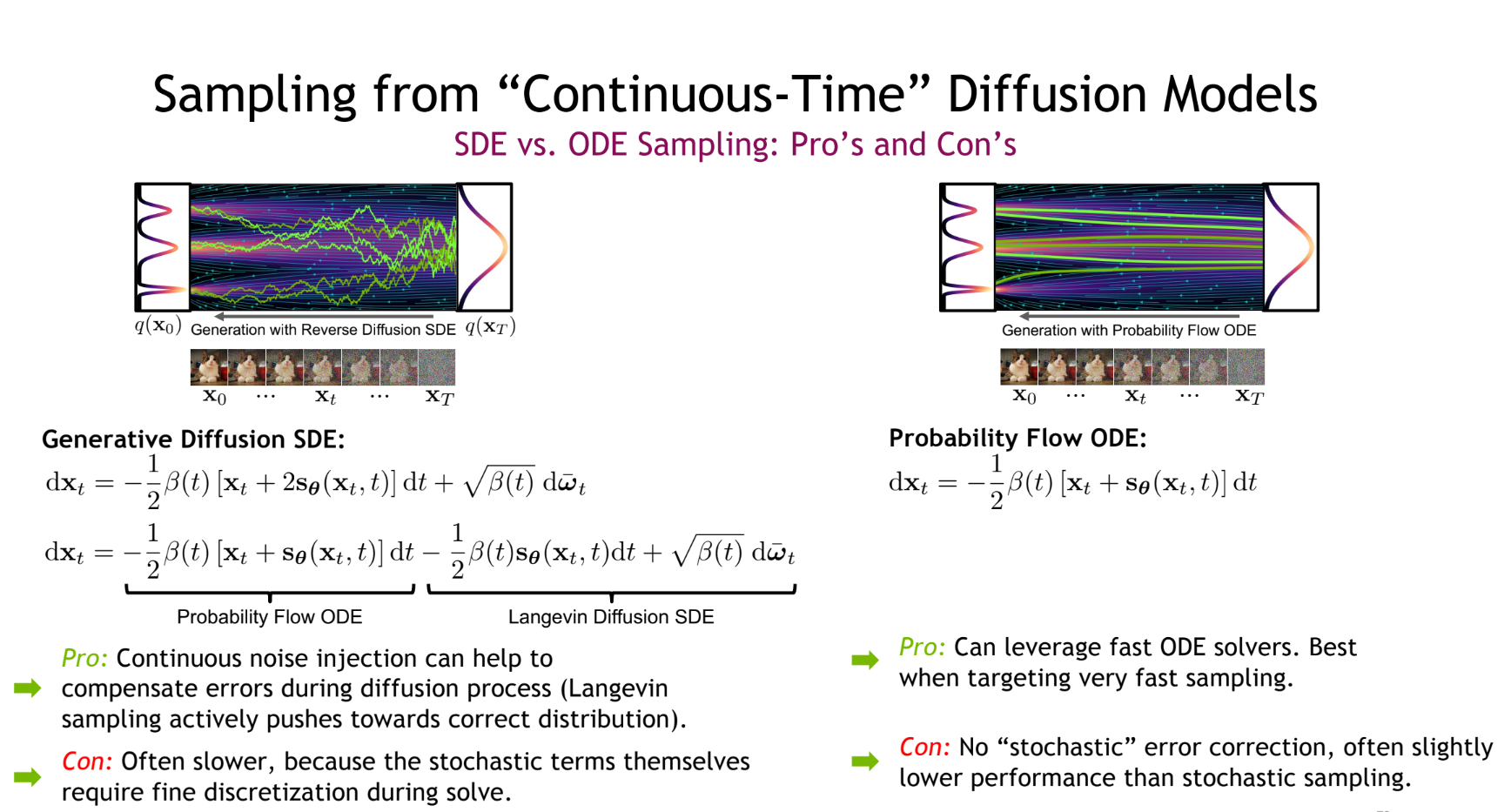
아래 수식처럼 노이징 프로세스를 테일러 급수를 이용하여 표현하면 x_t에 대해 Stochastic Differential Equation을 얻을 수 있음 (확률적인 미분 방정식).


이를 통해 reverse step도 아래 수식으로 정의 가능함
빨간색 부분인 score function을 아는게 핵심.

쉽게 구하면 좋겠지만, not tractable하기 떄문에 식을 변형하여 구함.
결과적으로, DDPM의 학습방식과 동일하게 됨. Diffusion과 Score-based는 같은 관계를 가지고 있다. 둘 다 SDE에 포함됨.
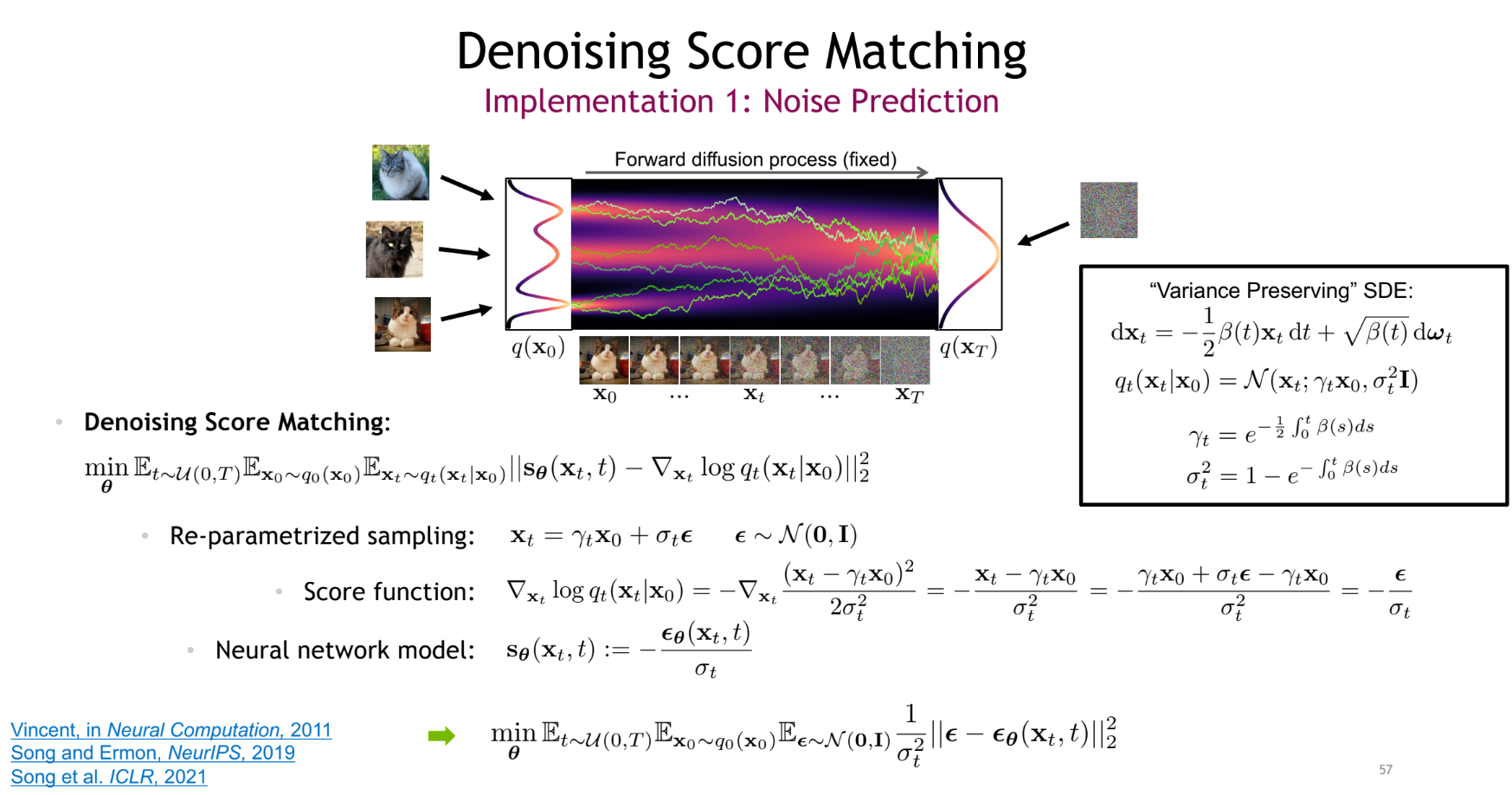
stochastic term을 만지면, deterministic 하게도 가능. (두 사이를 조절도 가능할 듯)
두 방식은 장단점이 있음.
4. Conditional Diffusion (Class-Guidance)
random한 자연스러운 이미지를 샘플링 하는게 아니라 원하는 이미지를 만드는 것이 목표
class 정보를 부여하면 그 class에 대한 이미지를 만들 수 있도록 함.
given x 에 대한 p(y|x)임 x는 text가 되기도 하고 autoregressive하게 만들 수 있도록 이미지의 부분을 주기도 하고 뭐든 줄 수 있음 정해진 형태의 x 가 있는건 아님
score model뿐만 아니라 classifier도 sampling에 영향을 끼치도록 한다.
결국 원하는 정보를 Diffusion process에 넣을 수 있다는 것이 핵심
아래 슬라이드를 참고해보도록 하자.


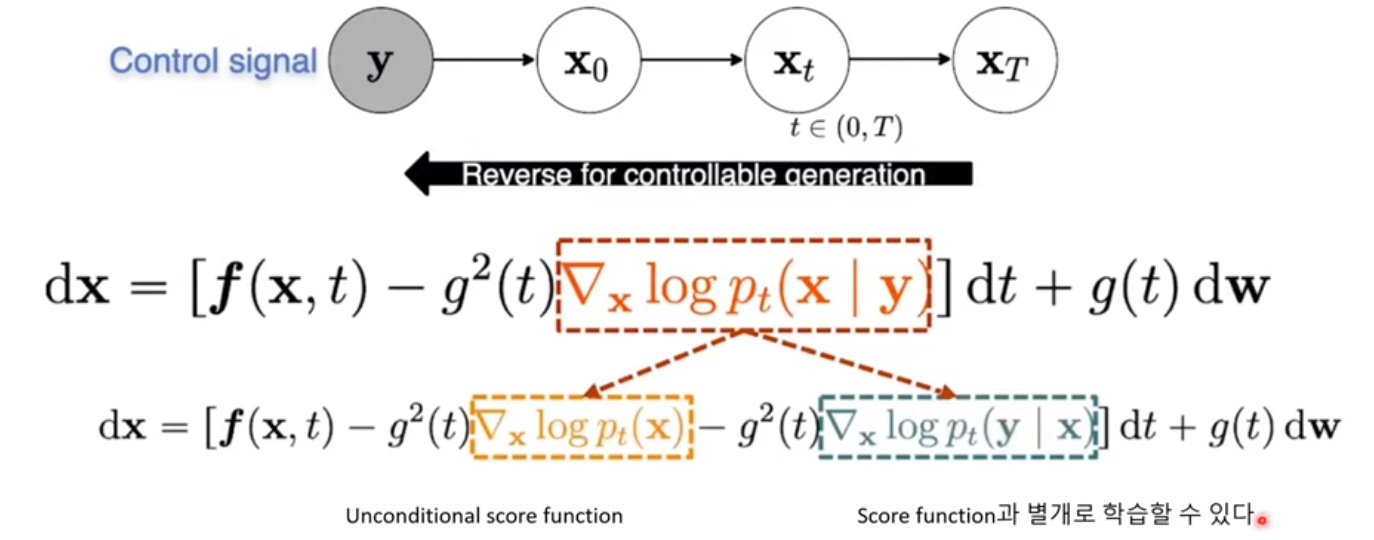
여기에 추가로 Unconditional diffusion에 대해서 Classifier가 있는 것과 동일하게 동작하도록 하는 것도 가능
이거는 학습하는 방법에서의 technic인 듯 (skip) pseudo label?
여기서는 class를 줄 수 있고, 그에 대한 weight를 조절할 수 있어서 class 정보가 있어도 생성가능, 없어도 생성가능한 점이 핵심인 거 같다.

Diffusion 프로세스 자체가 강력한 느낌
GAN과의 차이점을 및 장단점을 명확히 파악해야함



