https://wikibook.co.kr/reinforcement-learning/
파이썬과 케라스로 배우는 강화학습: 내 손으로 직접 구현하는 게임 인공지능
“강화학습을 쉽게 이해하고 코드로 구현하기” 강화학습의 기초부터 최근 알고리즘까지 친절하게 설명한다! ‘알파고’로부터 받은 신선한 충격으로 많은 사람들이 강화학습에 관심을 가지
wikibook.co.kr
해당 포스팅은 위의 책을 보고 정리한 내용이 주를 이룹니다.
이 포스팅에서 Neural Network(Deep Learning)에 대해서는 따로 설명하지 않겠습니다. 강화 학습과 더불어 또 하나의 큰 분야인데 강화 학습 주제에 곁들여 설명하기는 쉽지 않습니다. Nerual Network 부분을 모르신다면 다른 포스팅을 보시거나 관련 강의를 수강하시면 좋을 거 같습니다. 유튜브에 많은 Deep Learning 강의가 많이 존재하기 때문에 쉽게 찾으실 수 있을 겁니다.
또한 SARSA에 대한 설명은 아래 포스팅을 참고하시면 좋을거 같습니다.
2022.01.09 - [강화 학습] - 강화 학습 기본 - 시간차 학습(Temporal-Difference Learning) part 1. 살사(SARSA)
오늘 포스팅할 Deep SARSA는 Deep Nerual Network(DNN) + SARSA의 준말로 DNN를 접목시킨 알고리즘으로 비교적 최신의 내용을 다룬다고 볼 수 있습니다. 이제 강화학습 좀 안다고 할 수 있는 겁니다..
이전 포스팅을 보신 분들은 조금 의아할 수 있습니다. TD 방식으로 문제를 충분히 잘 푸는데 왜 굳이 Nerual Network까지 가지고 와서 쓰냐는 것이죠. 이 부분은 다이나믹 프로그래밍(DP)의 한계로 다시 넘어갑니다(아래 링크).
2022.01.05 - [강화 학습] - 강화 학습 기초 - 다이나믹 프로그래밍의 한계(Limitation of Dynamic programming)
이전 포스팅에서는 아래와 같이 3가지 DP의 한계를 알아봤습니다.
- 계산복잡도
- 차원의 저주
- 환경에 대한 완벽한 정보가 필요
그중 3번째 한계점은 지금까지 배운 몬테카를로, TD 방식으로 model-free 하게 학습할 수 있음을 보였습니다.
하지만 첫 번째와 두 번째는 크기가 더 큰 문제를 풀려고 할 때, 여전히 큰 골칫거리입니다. 하지만 그렇다고 5x5 그리드 월드에 갇혀있을 수 없는 노릇이죠.
그래서 제안된 방법이 Deep Nerual Network를 사용하는 방법입니다. Non-linear activation function을 사용한 Deep Neural Network은 이론적으로 일정 오차 범위 내에서 모든 함수를 Universal approximation이 가능합니다. 해당 내용 관련해서는 아래 미시간 대학교 저스틴 존슨 교수의 강의를 추천합니다. (추가로, 저 강의 시리즈 전체도 제가 들은 강의 중 가장 괜찮은 강의로 꼽습니다. 추가적인 컴퓨터 비전 공부를 하시는 분들에게 추천합니다.)
아래는 아주 간단한 Linear regression 예제입니다. 기울기 A와 Bias b라는 아주 적은 파라미터를 통해 많은 파란 점들의 경향을 어느 정도 오차 이내로 표현하였죠. 물론 아래 파란 점을 모두 기억하는 것이 가장 오차가 적겠지만, 앞서 말했듯 차원이 커지고, 문제가 복잡해지면 그 계산량은 기하급수적으로 늘어나기 때문에 이렇게 근사하는 방식은 필수적입니다(양자컴퓨터가 판을 바꿀까요?).
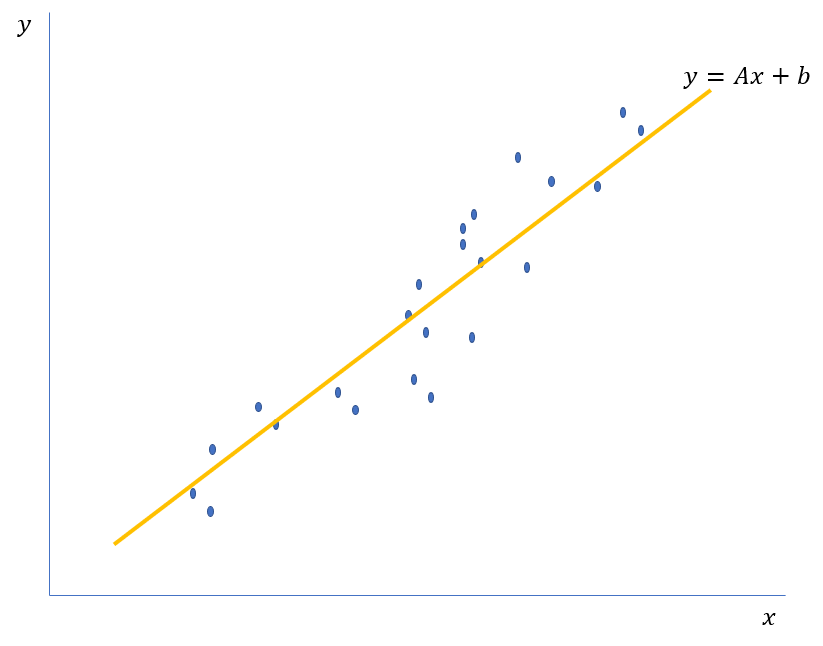
여기에 Non-linear activation function을 사용하게 되면 Neural Network는 비선형적인 데이터에 대해서도 근사가 가능하게 되죠. 따라서, Neural Network의 Universal approximation이 가능한 성질을 이용하여 바둑과 같은 매우 복잡한 상태를 비교적 적은 파라미터로 나타낼 수 있는 함수 형태로 근사할 수 있게 되는 겁니다. 더 복잡한 문제에도 충분히 도전이 가능하게 되는 셈이죠.
이 개념만 알고 들어가면 Deep SARSA는 매우 간단해집니다. 단지 Neural Network을 SARSA업데이트에 적용한 것이죠.
이제 책에서 드는 예시를 가져와 본격적으로 Deep SARSA를 설명해보겠습니다. 아래는 더 복잡해진 그리드 월드를 보여줍니다. 장애물이 움직이는 환경에서 에이전트는 도착까지 가야 되는 문제인 것이죠. (*이때 상태 S_t에서 어떤 A_t를 취할지는 Decaying ε-greedy policy를 사용합니다!)
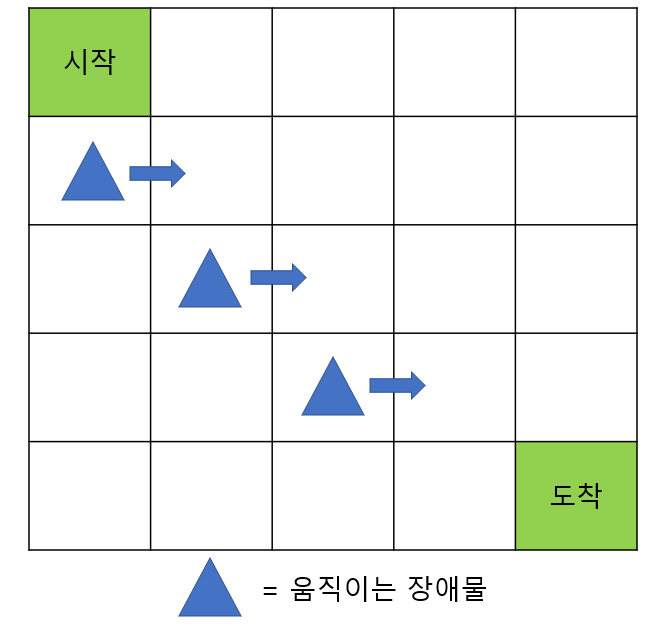
가장 먼저 해야 하는 일은 문제가 바뀌었으니 MDP를 재 정의하는 것입니다. MDP의 5요소는 상태, 행동, 보상 함수, 상태 변환 확률, 할인율이 있지만 같은 그리드 월드이므로 상태에 대한 재정의 만 요구됩니다. 이전에는 자신의 위치만 알고 있으면 다음 행동을 결정하는데 문제가 없었지만, 지금은 아닙니다. 장애물에 대한 정보가 있어야 적절한 행동을 결정할 수 있죠. 책에서는 상태를 다음과 같이 재정의 합니다. 총 15가지 요소가 한 상태를 나타내게 되는 것이죠. (도착지점 x, y, 라벨 그리고 (장애물 x, y, 라벨, 속도) x3)
- 에이전트에 대한 도착지점의 상대 위치 x,y (2가지 원소)
- 도착지점의 라벨
- 에이전트에 대한 장애물의 상대위치 x, y(2가지 원소)
- 장애물의 라벨
- 장애물의 속도
위와 같이 문제를 풀기 위한 특징을 추출하는데 문제가 복잡해질수록 핵심이 되는 특징을 추출하는 것, 그리고 수학적으로 모델링하는 것이 중요한 부분인 거 같습니다.
이제 수식을 보겠습니다.
먼저 이전에 봤던 SARSA에서의 업데이트 수식입니다. 아래와 같이 각 상태 S_t, S_t+1 그리고 각 행동 A_t, A_t+1에 저장돼있는 각 값들을 저장하고 있죠.
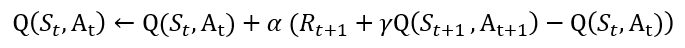
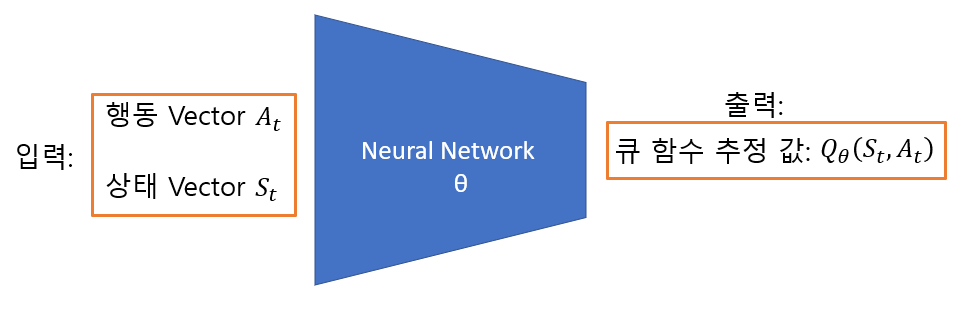
하지만 Deep SARSA에서는 이러한 정보들이 모두 Neural Network 속 파라미터 θ에 근사됩니다. Q함수를 업데이트를 목표로 하고 있기 때문에 아래와 그림과 같은 형태죠. (단, 책에서 제공하는 코드는 상태 벡터를 입력으로 받아 모든 행동에 대한 Q 함수를 출력합니다. 그 후, 실제 한 행동과 매칭 되는 Q 함숫값만을 가지고 학습을 진행하죠.)
이제 Deep SARSA에서 Neural Network가 어떤 역할을 하는 건지 감이 좀 오셨으리라 믿습니다. 그렇다면 Neural Network는 어떻게 학습이 진행될까요? 바로 지도 학습 기반으로 이루어 집니다. 강화학습이 비지도 학습인데 어떻게 지도학습 기반이 가능하냐 하실 수 있는데, 이는 SARSA의 업데이트 수식에 그 힌트가 있습니다.
업데이트 수식에 α로 묶여있는 항 R_(t+1)+γQ_θ (S_(t+1),A_(t+1))-Q_θ (S_t,A_t )는 기존 Q함수를 업데이트하는 역할을 합니다. SARSA에서는 앞서 설명했던 것과 같이 충분히 많은 에피소드를 통해 학습이 되면 수렴합니다. 즉, R_(t+1)+γQ_ (S_(t+1),A_(t+1))항과 Q(S_t,A_t )항의 차이가 없어지는 것이죠(또는 매우 근소).
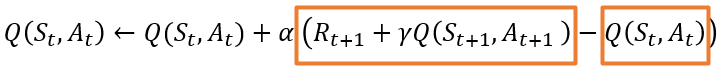
현재 상태 S_t에서 A_t에 대한 Q함수의 값이 그다음 상태 S_t+1에서 A_t+1에 대한 값과 일치하는지 보는 거죠(A_t에 의한 R_t+1와 할인율 또한 고려됩니다.) 몬테카를로 방식이나 TD 방식에서는 충분히 많은 에피소드를 통해 학습했으면 이와 같이 수렴합니다. 바로 이 부분을 이용해서 Neural Network를 지도 학습으로 학습시킬 수 있습니다. R_(t+1)+γQ(S_(t+1),A_(t+1))항과 Q(S_t,A_t )항의 차이를 줄이도록 학습하는 것이죠.
이것이 바로 Deep SARSA에서 쓰이는 Neural Network의 Loss Function이 됩니다. 그 수식은 아래와 같이 제곱을 취해 사용합니다. 이 Loss Function을 이용하여 Deep SARSA는 역시 충분히 많은 에피소드를 통해 어떤 S_t에서 A_t를 취했을 때에 대한 적절한 Q-함수를 계산해주는 Deep Neural Network를 학습시킬 수 있습니다. (이때 Neural Network의 θ 파라미터에 의해 추정된 값이므로 Q_θ표기 를 사용합니다.)
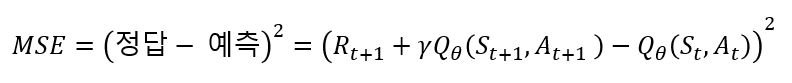
정리하자면, 복잡한 문제에 대해 SARSA의 수식에서 착안해 Neural Network를 학습시켜 가치 함수를 계산(근사)하게 하여 문제를 푼 것이 Deep SARSA입니다. 이제 우리는 이 메커니즘을 통해 강화 학습은 이제 더 복잡한 차원 그리고 상태의 문제도 풀 수 있게 되었다고 볼 수 있습니다!
여기까지 왔으면 Deep SARSA를 이해하는데 필요한 정보는 다 설명했다고 볼 수 있습니다. 하지만 저도 한번 읽고서 이 정보가 지식이 되지는 않았는데요. 아무래도 여러 가지 개념들이 같이 섞여있어 이해가 힘드실 수도 있습니다. 그래서 Deep SARSA를 이해하기 위한 키워드를 나열하고 이 포스팅을 마치겠습니다. 한 키워드라도 제대로 떠오르시지 않는다면, 그 부분에 대해 공부하시면 이해가 되시리라 믿습니다.
- Deep Neural Network의 학습 메커니즘(a.k.a Deep Learning, 포스팅에서 다루지 않음)과 Universal approximation으로 상태를 효율적으로 나타낼 수 있음.
- 몬테카를로 근사 -> 충분히 많은 에피소드로 참값에 가까워질 수 있다.
- Temporal-Difference Learning과 SARSA -> 실시간으로 업데이트되는 학습 방식 그리고 그것 또한 참 값에 가까워진다.
- 이 포스팅에서 R_(t+1)+γQ_θ (S_(t+1),A_(t+1))항과 Q_θ (S_t,A_t )항의 차이를 줄이는 것이 Loss Function(문제를 최적화 하는데)으로 사용될 수 있다.
감사합니다.
'강화 학습' 카테고리의 다른 글
| 강화 학습 - DQN (1) | 2022.01.12 |
|---|---|
| 강화 학습 - 정책 기반(Policy-based) 강화 학습, REINFORCE 알고리즘 (0) | 2022.01.11 |
| 강화 학습 기본 - 시간차 학습(Temporal-Difference Learning) part 2. 큐 학습(Q-Leaning) (0) | 2022.01.10 |
| 강화 학습 기본 - 시간차 학습(Temporal-Difference Learning) part 1. 살사(SARSA) (1) | 2022.01.09 |
| 강화 학습 기본 - ε-탐욕 정책(ε-greedy Policy) 그리고 ε-decay (0) | 2022.01.07 |



