- REINFORCE 알고리즘https://wikibook.co.kr/reinforcement-learning/
파이썬과 케라스로 배우는 강화학습: 내 손으로 직접 구현하는 게임 인공지능
“강화학습을 쉽게 이해하고 코드로 구현하기” 강화학습의 기초부터 최근 알고리즘까지 친절하게 설명한다! ‘알파고’로부터 받은 신선한 충격으로 많은 사람들이 강화학습에 관심을 가지
wikibook.co.kr
해당 포스팅은 위의 책을 보고 정리한 내용이 주를 이룹니다.
또한, 이 포스팅에서 Neural Network(Deep Learning)에 대해서는 따로 설명하지 않겠습니다.
- 가치 기반 방식과 정책 기반 방식의 차이
들아가기 전에 지금까지 로드맵을 그려보았습니다. 책의 내용에서 어느 정도 흐름이 있다고 생각했는데, 이번 포스팅(아래 그림. 빨간 화살표)은 "갑자기 이게 왜 나오지?"라는 의문이 들게 했습니다. 찾아본 결과, 강화 학습의 여러 갈래를 병렬적으로 설명하고 있기 때문이었습니다.
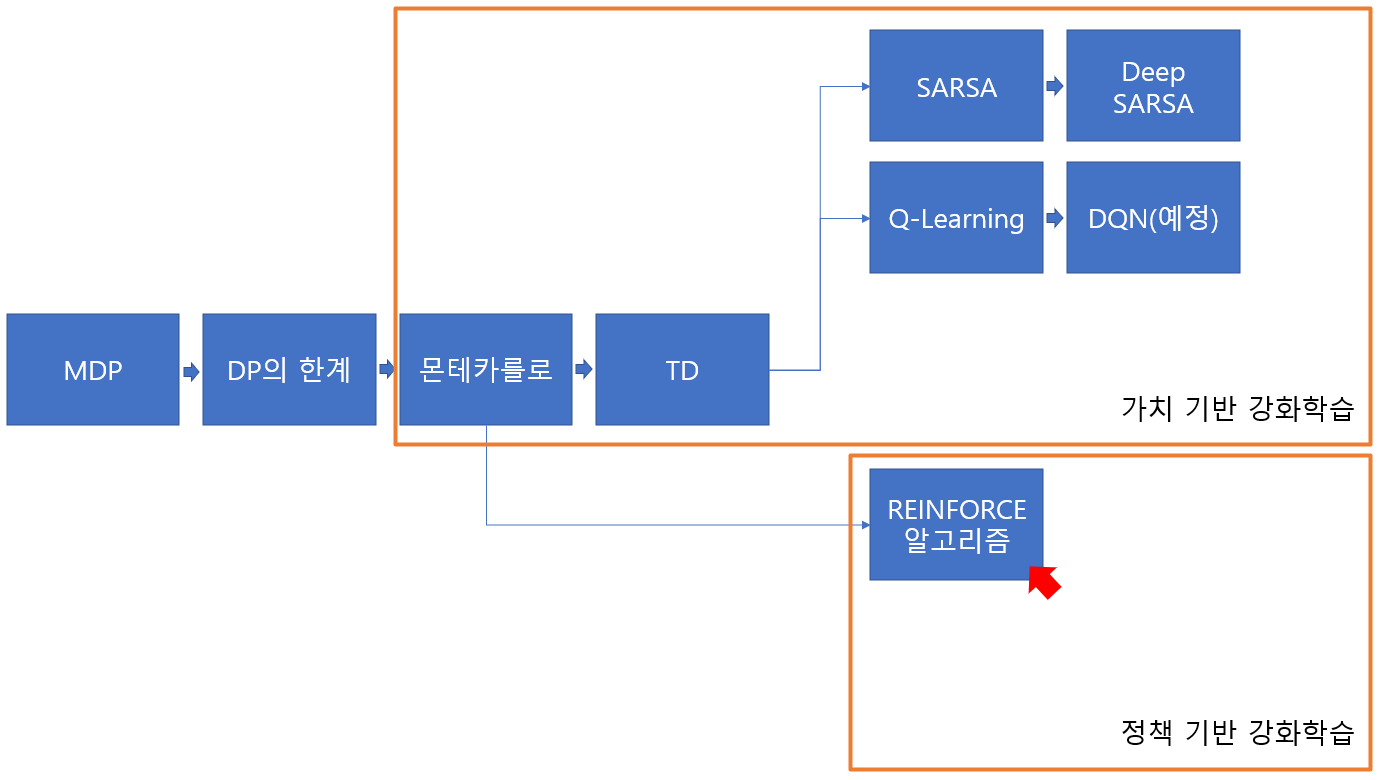
따라서, 오늘 내용은 최근 포스팅 Deep SARSA와 같이 Deep Nerual Network를 활용하지만 가치 함수의 업데이트에 중점을 두지 않고 정책을 중심으로 강화 학습을 접근합니다.
그럼 두 방식의 차이는 뭐냐? 제가 가치 기반과 정책 기반의 차이를 이해한 바는 이렇습니다.
- 가치 기반 방식은 어떤 상태에서 어떤 행동의 가치를 계산(근사)합니다.(참고로 가치기반 방식에서 정책은 Decaying ε-greedy policy입니다.)
- 정책 기반 방식은 어떤 상태에서 어떤 행동을 해야 할지를 계산(근사)합니다.
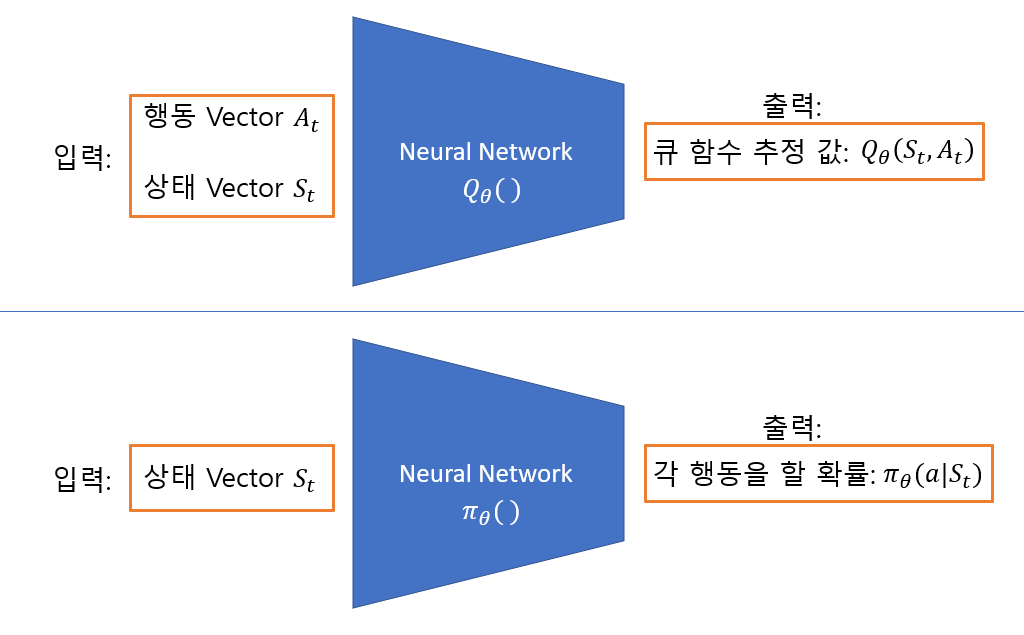
- 정책 기반의 Nerual Network의 출력
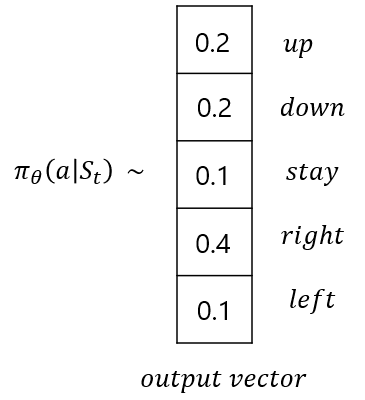
위의 그림에서 확인할 수 있듯, 정책 기반의 Nerual Network(이하 정책 신경망)는 π_θ(a|S_t)를 출력으로 놓습니다. 이 π_θ(a|S_t)의 의미는 NN의 파라미터 θ를 통해 연산된 각 행동에 대한 확률(추정) 값입니다. 이는 정책의 정의가 기본적으로 확률로 되어있기 때문이죠. (코드 상에서는 출력 layer에 Softmax함수 사용합니다.)
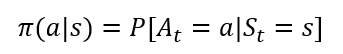
- 정책 기반 방식의 Objective Function
"강화 학습의 목표는 누적 보상을 최대로 하는 최적 정책을 찾는 것"이라고 책에 나와있습니다. 그럼 어떻게 정책 신경망이 최적 정책을 근사하도록 학습을 시킬 수 있을까요? 우선 명확한 Objective Function이 필요합니다. Objective Function을 통해 gradient가 나오고 모델 파라미터 θ가 업데이트될 수 있기 때문이죠. 앞으로 이 Objective Function을 J(θ)로 표현하겠습니다. 책에서는 아래와 같이 목표 함수를 가치 함수를 써서 정의합니다.
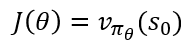
책에서는 "만일 에피소드의 끝이 있고 에이전트가 어떤 특정 상태 s_0에서 에피소드를 시작하는 경우 목표 함수는 상태 s_0에 대한 가치 함수라고 할 수 있니다."라고 설명하고 끝이 납니다. 저는 바로 이해되지는 않았는데요. 상태 가치 함수 v의 수식을 다시 보겠습니다. 아래 수식과 같이 v 함수는 상태 s에서 정책 π를 따랐을 때의 기댓값이었죠.
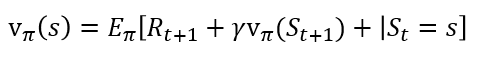
다시 정리해보겠습니다. "강화 학습의 목표는 누적 보상을 최대로 하는 최적 정책을 찾는 것이다." 이 말을 재구성하면 "정책 기반 방식의 Objective Function은 시작점에서부터 에피소드 종료 시 누적 보상이 최대로 하는 π_θ를 찾는 것이다."로 볼 수 있습니다. 이 시작점에서부터 에피소드 종료 시 누적 보상이 시작점에서 π_θ정책을 따랐을 때의, 상태 가치 함수인 𝑣_(𝜋_𝜃)(𝑠_0)이 되는 것이죠.
따라서, 정책 신경망(=π_θ)의 출력을 따랐을 때, 𝑣_(𝜋_𝜃)(𝑠_0)가 최대가 되게 하는 정책 신경망의 파라미터 θ를 해야 되는 것이죠. 그리고 정책 신경망의 학습 과정은 누적 보상 𝑣_(𝜋_𝜃)(𝑠_0)를 최대화해야 하기 때문에 강화 학습의 목표는 아래와 같이 표현됩니다.
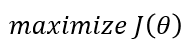
- 정책 신경망의 Gradient와 REINFORCE 알고리즘 (수식 多)
정책 신경망의 학습의 위해서는 θ를 업데이트하기 위한 gradient가 요구됩니다. 아래와 같은 수식으로 표현됩니다. 이때 α는 Learning Rate입니다.
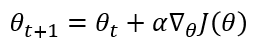
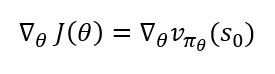
Gradient가 요구되는 것은 미분 가능해야 한다는 것인데, 책에서는 이 부분을 조금 더 다룹니다. 우선 리처드 서튼의
Policy Gradient Methods for Reinforcement Learning with Function Approximation(NIPS, 1999) 논문에 따르면 위에서 본 목표 함수의 미분은 아래의 수식같이 정리가 가능하다고 합니다. 이때 d_(π_θ)는 s라는 상태에 에이전트가 있을 확률인 상태 분포를 나타낸다고 합니다.
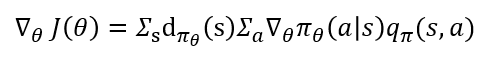
여기서 π_θ (a│s)/π_θ (a│s)를 추가해 줍니다. 식을 다른 모양으로 정리하기 위해서입니다.
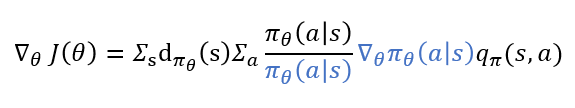
이때 로그함수의 미분(좌측 파란색 부분)을 이용하여 위의 수식을 아래와 같이 정리합니다.
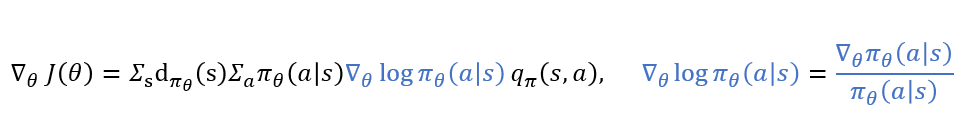
위의 식을 기댓값의 형태로 아래와 같이 나타낼 수 있는데요. 이는 초록색으로 칠해진 부분이 에이전트가 어떤 상태 s에서 행동 a를 선택할 확률을 의미하기 때문이라고 책에 나와있습니다. 그 아래 기댓값의 정의를 가져와서 좀 더 쉽게 볼 수 있도록 했습니다. "어떤 상태 s에서 행동 a를 선택할 확률" 즉 p_i꼴로 나타내 지기 때문에 가능한 것이죠.
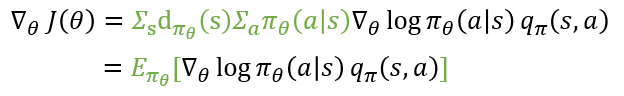
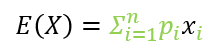
이전에 포스팅한 몬테카를로 근사를 통해 기댓값은 충분히 많은 샘플링으로 대체된다는 것을 이미 알아봤습니다. 그럼 기댓값 괄호 안에 있는 항이 우리가 학습을 위해서 알아야 하는 값임을 이제 우리는 알게 되었습니다.
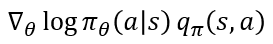
하지만 여기서 또 문제가 있습니다. 정책 신경망은 π_θ를 통해 π_θ (a│s)의 값을 알 수 있습니다. 하지만 그 옆에 행동 가치 함수 q_π(s,a)를 구할 수 없습니다. 정책 π_θ는 가지고 있지만 가치 함수에 대해서는 고려하지 않았기 때문이죠. 따라서 q_π(s,a)를 다른 적절한 항으로 대체해야 합니다. 여러 방법 중 반환 값 G_t로 대체하는 것이 바로 REINFORCE 알고리즘입니다. 아래 수식과 같이 업데이트가 표현되는 것이죠. 여기서 맨 아래가 REINFORCE 알고리즘에서 학습을 나타내는 수식입니다.
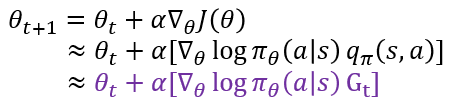
REINFORCE 알고리즘 학습은 한 에피소드마다 실제 얻은 보상들..., G_t-1, G_t, G_t+1,..로 학습이 이루어집니다. 이때 각 반환 값들은 에피소드가 끝나야 계산이 가능한데요. 그렇기 때문에 몬테카를로 폴리시 그레디언트라고도 한다고 합니다(TD 방식이 아니죠).
- REINFORCE 알고리즘 학습 디테일
사실 REINFORCE 알고리즘의 개념은 위에서 언급했는데요. 이 파트에서는 책에서 나온 구현 상에서의 세부적인 정보를 추가로 언급하려고 합니다.
1. 먼저, 신경망 자체가 정책이고 그 출력이 확률을 나타내기 때문에, Deep SARSA와 다르게 Decaying ε-greedy policy 같은 임의의 탐험을 할 필요가 없습니다. 신경망을 학습하는 과정 자체가 확률적으로 탐험을 하는 정책이기 때문이죠.
2. 한 에피소드가 끝난 후 정산을 통해 구해진 각 S_t에 대한 G_t는 이미 계산된 상수입니다. 따라서 아래 식처럼, θ로 같이 미분될 수 있죠. 그냥 같이 곱해줘서 이 Loss로 Back-propagation 시키면 됩니다.
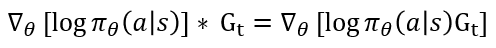
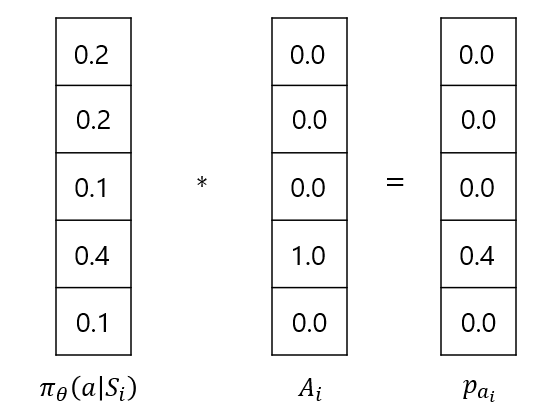
3. Object Function의 코드상 구현은 Cross-Entropy로 구현됩니다. 이때 y_i는 i 시점에서 실제 한 행동을 나타내고, p_i는 π_θ (a│s)에 해당하는 실제 한 행동 a_i의 확률 값으로 표현 가능합니다. 실제 한 행동을 나타내는 벡터는 one-hot vector이므로 곱하면 결국 a_i의 확률에 로그가 취해지는 것과 같죠. 아래 수식과 그림을 보면 이해가 되시리라 생각합니다.
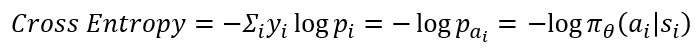
4. 보통의 Nerual Network이 경사"하강"법을 통해 Objective function을 최소화하는 방향으로 학습하지만, 정책 신경망은 앞서 언급한 거 같이 Objective function 최대화하는 방향으로 경사"상승"법을 통해 학습합니다. 따라서 위에서 계산한 Cross Entropy에 마이너스 부호를 둔 채로 반환 값 G_t를 곱해 경사 하강법을 시키면 그 의미가 일맥상통한 것이죠(Framework가 경사 하강법을 통해 학습하도록 돼있어서 이렇게 시도하는 거 같습니다.).
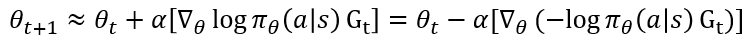
5. 사실 중요한 포인트가 하나 더 있습니다. Deep SARSA포스팅에서 사용했던 그리드 월드 예제를 다시 보겠습니다. 여기서는 매 타임 스텝마다 (-0.1)의 보상을 주는 건데요. 이는 시간이 지날수록 또는 한 에피소드가 오래 걸릴수록 보상이 감소되게 하는 것입니다.
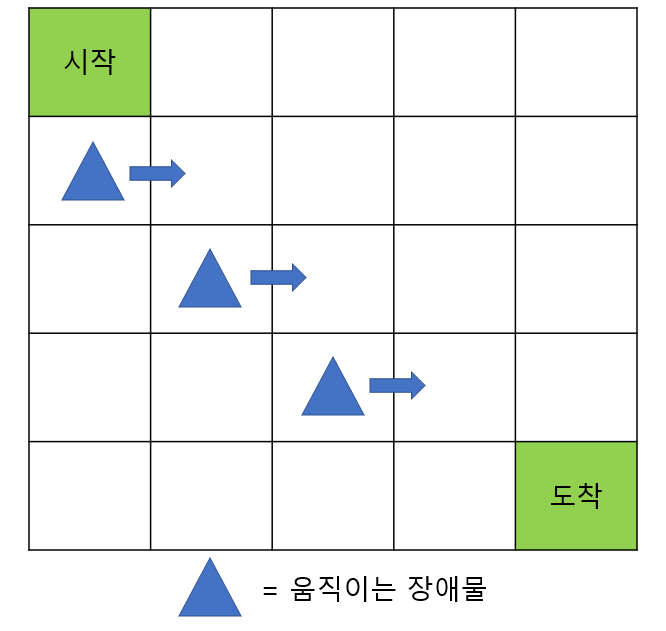
이는 학습 초반에 생기는 문제를 해결하기 위함인데요. 학습 초반에 에이전트는 도착점에 무사히 도착하기보다 장애물에 부딪히는 경우가 더 많이 생깁니다. 장애물에 많이 부딪히게 되면 도착을 하더라도 그 보상이 음수가 될 수도 있습니다. 이렇게 되면 에이전트는 도착을 하는 것이 아닌 가만히 있는 게 가장 큰 보상을 받게 되는 최적의 정책이 될 수도 있는 것이죠. 이 점을 보완하기 위해 타임 스텝마다 (-0.1)의 보상(페널티)을 주어 가만히 있는 것을 지양하도록 한 것입니다.
바로 위와 같이 각 문제에 알맞게 추가적인 보상 또는 페널티를 넣어주는 안목도 강화 학습을 진행하는 데 있어서 중요한 덕목이 아닌가 싶습니다.
이렇게 정책 기반의 강화 학습에 대해 알아보았습니다.
감사합니다.
'강화 학습' 카테고리의 다른 글
| 강화 학습 - A2C, Continuous A2C (2) | 2022.01.13 |
|---|---|
| 강화 학습 - DQN (0) | 2022.01.12 |
| 강화 학습 - 딥 살사(Deep SARSA) 알고리즘 (0) | 2022.01.10 |
| 강화 학습 기본 - 시간차 학습(Temporal-Difference Learning) part 2. 큐 학습(Q-Leaning) (0) | 2022.01.10 |
| 강화 학습 기본 - 시간차 학습(Temporal-Difference Learning) part 1. 살사(SARSA) (1) | 2022.01.09 |



